空間ベクトル変調 - Space Vector Modulation -
三相インバータは，直流中点基準電圧 vUVW-O=[vUO,vVO,vWO]T を出力します．この電圧を相電圧で捉えると，インバータ自身のスイッチングによって７通りのベクトルをとることができます． そして，空間ベクトル変調という手法により，これらの限られたベクトルから任意の電圧ベクトルを生成することができます． こうして得られたベクトルがモータの駆動に利用されます．
ここでは，任意の電圧ベクトルを生成する手法である空間ベクトル変調の原理について解説します．
（著者：2019年度5年 杉山康恭）
三相インバータと空間ベクトル
まず vUVW-O とは，三相インバータ（図１）の各相において，上側（P：positeve）と下側（N：negative）のうち一方をオンにする制御を行って得られる電圧です．そして，モータの三相巻線の対称性により，この vUVW-O の各成分からコモンモード電圧
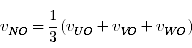...(1)
を差し引くと相電圧 vUN, vVN, vWN が得られます．相電圧は，U相巻線を基準にそれぞれ 0, 120, -120 deg の方向を向く電圧ベクトルであると考えることができます． この方向に注意して3つのベクトルを合成したものが空間ベクトルです．
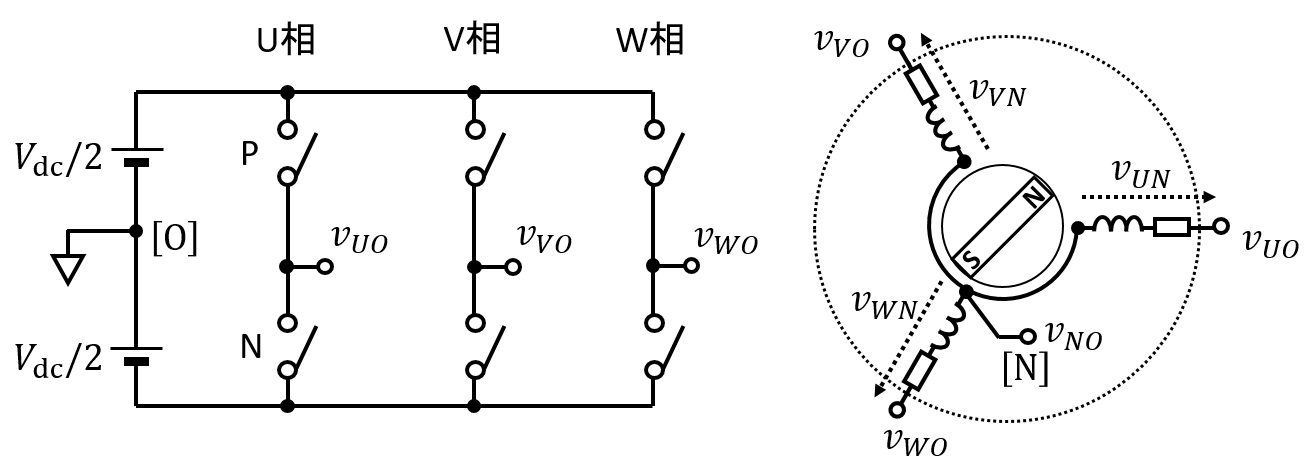...【図１】三相インバータ
例えば，インバータのオンであるスイッチが，U相:上側,V相:下側,W相:下側（UP,VN,WN）の場合，U軸方向を向くベクトル V1 が得られます（図２）．
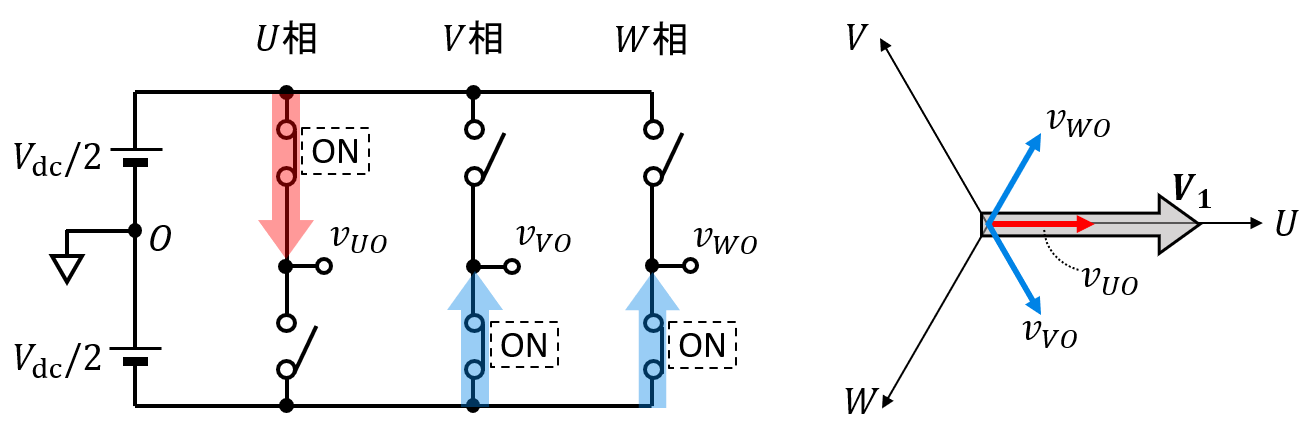...【図２】空間ベクトル V1
- [注意] 図２では直流中点基準電圧を合成しています．本来は相電圧を合成するべきですが，結果が変わらず，相電圧よりも視覚的に扱いやすいため，基準点を O としています．
上記の考え方を一般化します．各相のスイッチ（P側とN側）は必ず一方がオン，他方がオフであることを考慮すると，スイッチングの組み合わせは全部で８通り存在し，空間ベクトルは V0～V7 の８種類ののいずれかをとります（表１）．これらを図示すると図３(a) のようになり，さらに電力を一定に保つ絶対変換
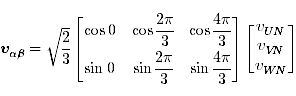...(2)
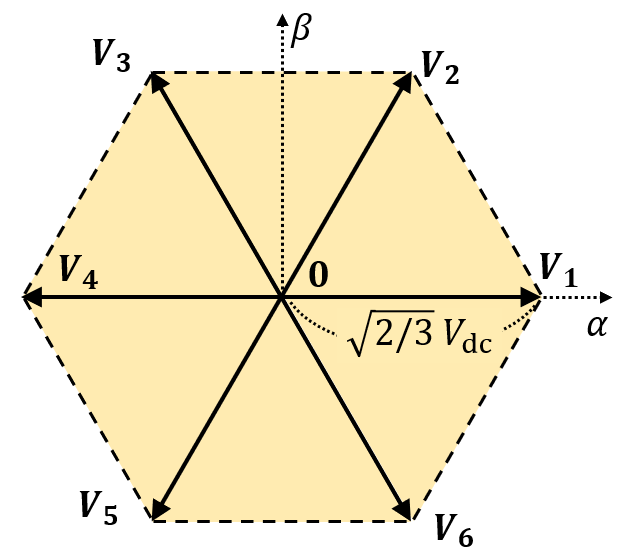
を行った場合は図３(b) のようになります． このように，空間ベクトルは瞬時的には原点または正六角形の頂点しか示すことができません．
...【図３】出力可能な空間ベクトル
空間ベクトルの重ね合わせ
前節では，空間ベクトルが離散的な７点しか示せないことを説明しました． 本節では，そのような空間ベクトルを重ね合わせることによって，α-β軸上で任意の位相や振幅を持つ電圧ベクトルを実現できることを説明します（実際には，振幅に上限があります．その上限値は位相の関数となり，原点から正六角形の周上の点までの距離を表します．）．
ここでは，簡単な例としてα-β軸電圧位相 θvαβ が 0≦ θvαβ＜60 deg の範囲にある場合を想定します．そして， vαβ に近い３つの空間ベクトル V1,V2,V0(=0) を用いて， vαβ を重ね合わせ
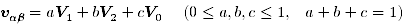...(3)
で表現できると仮定します．この式の図形的な意味を考えてみます．まず， V0=0, a+b=1-c に注意して上式を
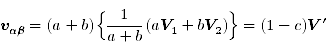...(4)
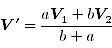...(5)（便宜のため分数表記）
と変形します．すると，V', vαβ はそれぞれ次のように解釈できます（図４）．
- V' ...... V1 と V2 を b：a の比に内分するベクトル
- vαβ ...... V' の長さを (1-c) 倍に縮小したベクトル
つまり， a と b は位相調整， c は振幅調整の役割を持ちます．
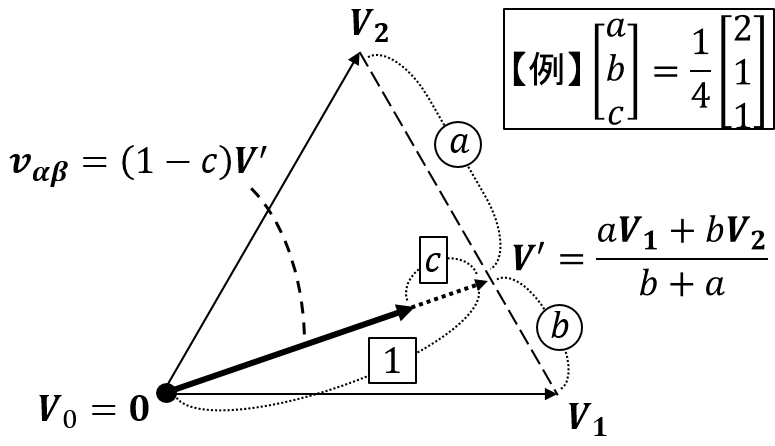...【図４】空間ベクトルの重ね合わせ
ところで，任意の vαβ を出力する場合，係数は当然非整数になり得ます．しかし，空間ベクトルはそれに対応するベクトルを瞬時的には出力できません． そこで，空間ベクトル変調では，係数 a, b, c をベクトルの長さではなく，ベクトルの出力時間の比率と捉えます．
つまり，ある時間間隔 T[s] において，インバータが V1,V2,V0 をそれぞれ aT, bT, cT[s] 間出力するするようにベクトルを切り替えます．そして，それを時間 T で平均化したものが vαβ となります（比率として考えることが，(3)式で 0≦a,b,c≦1，a+b+c=1 とおいた理由です）． ここで，時間 T は制御周期と呼ばれ，スイッチング損失などの現実的な問題を考慮した上で任意に決めることができます．
- [注意] 平均をとるという変調方法から， vαβ が出力可能な領域は V1～V6 の終点で作られる正六角形の周とその内部に限定されます（図５）．よって， vαβ の指令が六角形の外部にある場合は，実際の出力が指令を満足できない状態（電圧飽和）となります．
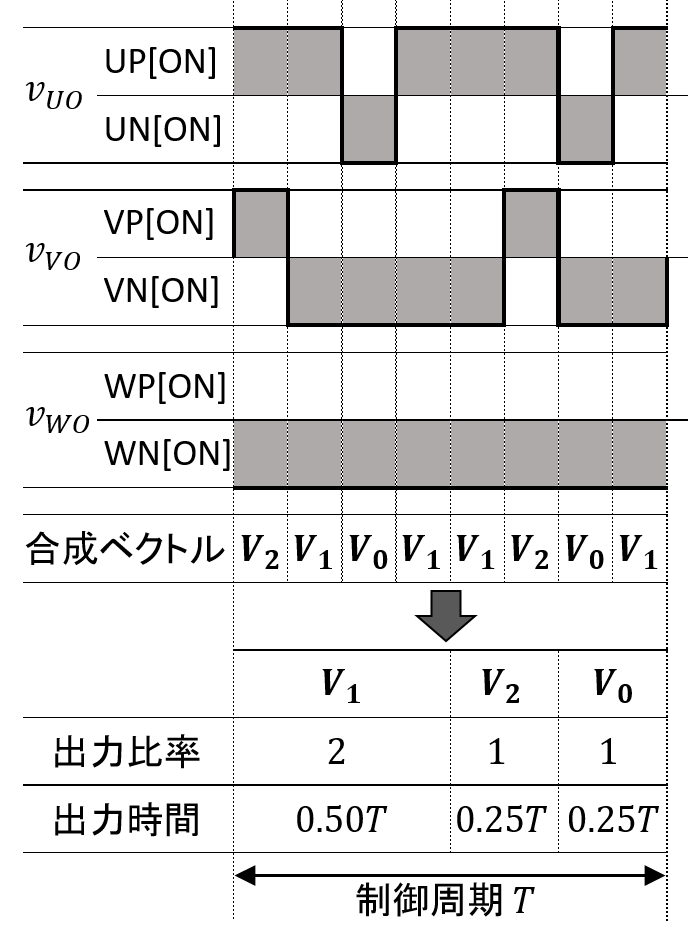
また，a, b, c は１周期を通してみたときの時間比率なので，比率が保たれていれば周期内のベクトルの並びには任意性があります（ベクトルの並べ替えを，専門用語でパルスシフトといいます）．例えば先程の図４は (a, b, c) = (0.50, 0.25, 0.25) として得られるベクトルを示していますが，これを実現するベクトルの並びは多数存在し，その一例として図６のようなものがあります．
【図５】電圧ベクトルの出力可能範囲 【図６】制御周期内でのベクトルの切り替え
重ね合わせの係数の導出
前節では，重ね合わせの意味の理解を容易にするために，３つの空間ベクトルの出力時間比率 a, b, c を決めることでベクトル vαβ が定まると説明しました．本節では反対に，任意のベクトル vαβ を重ね合わせで実現するための係数 a, b, c の求め方を説明します（前節と同じ場合で考えます）．
まず，空間ベクトルを列ベクトル表記すれば，(3) 式は
- [再掲] 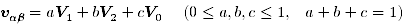...(3)
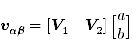...(6)
と変形することができます（※ V0=0 ）．さらに，ベクトルを成分表示すれば，次の連立方程式が得られます（空間ベクトルは絶対変換後の状態を表します）．
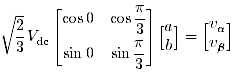...(7)
この係数行列は正則なので解が一通りに定まり， a, b を求めることができます．そして c=1-a-b から c も求めることができます．
重ね合わせの係数の導出（一般化）
最後に，任意の位相角 θvαβ をもつ電圧ベクトル vαβ を実現する方法を説明します．
これまでの例と同様に， vαβ はそれに近い３つの空間ベクトルを用いて実現します．そのうち１つは V0=0 です．残りの２つの選び方を数学的に表現します．
まず六角形を６個の三角形に分割し，各三角形で表される領域をセクタ (0～5) とします（図７）．
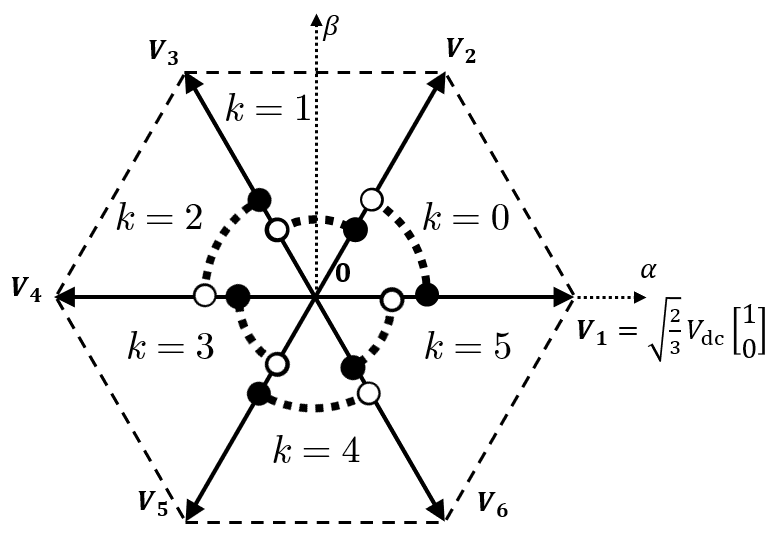...【図７】セクタ番号 k の定義
セクタ番号 k は，床関数を用いて
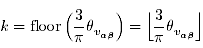...(8)
と表現できます．
すると， vαβ がセクタ k に属せば，用いる空間ベクトルは V-:=Vk+1, V+:=V(k+1 mod 6)+1,V0 となります（添え字に注意）．
次に，３つの空間ベクトルの出力時間の比率を a, b, c とおき， vαβ を重ね合わせ
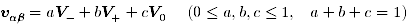...(9)
で表現します．さらに， V0=0 に注意して上式を
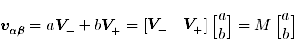...(10)
と変形します．ここで，係数行列
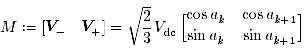...(11)
中の角 ak, ak+1 は，それぞれ V-, V+ の位相で，次のように定義されます．
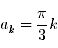...(12)
また，係数行列は，行列式の値が
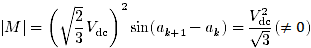...(13)
となるため，常に正則で逆行列が存在します．
したがって， a, b は次のように求めることができ， c(=1-a-b) も定まります．
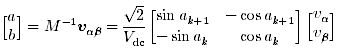...(14)
参考文献
- *[1]
- 電気学会・センサレスベクトル制御の整理に関する調査専門委員会：ACドライブシステムのセンサレスベクトル制御，pp.46-54
