拡張誘起電圧オブザーバ

回転子の位置推定法の一つに，拡張誘起電圧オブザーバを利用する方法があります．拡張誘起電圧オブザーバとは，回転子の位置情報を持った拡張誘起電圧（EEMF：Extended Electromotive Force）という状態量を， 抵抗・インダクタンスのように事前に測定することのできるモータパラメータと，電圧・電流といったセンサ等によって取得可能な物理量から，動的に推定する方法です．そして，推定した拡張誘起電圧から，回転子の位置情報を得て，モータの電流や速度の制御を行う方法が，拡張誘起電圧オブザーバに基づく位置・速度センサレス制御です．

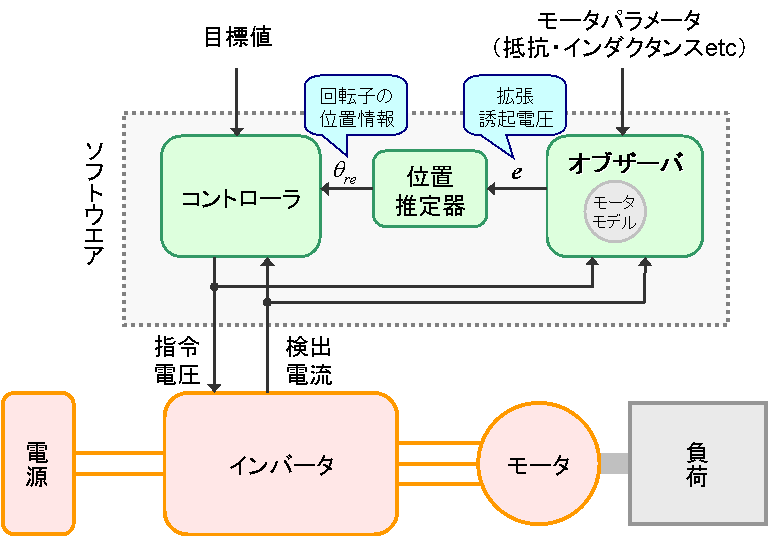
最小次元オブザーバの構成

拡張誘起電圧モデルのページで紹介した固定座標α-β軸上の拡張誘起電圧モデルを再掲します．

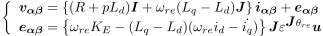...(1)

位置情報を持った拡張誘起電圧を推定するためにオブザーバ（状態観測器）を構成します．まず拡張誘起電圧モデルを状態方程式の形に変形します。 (1)第1式の電流微分項が左辺に来るように変形すると，

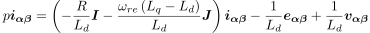...(2)

となり，また(1)第2式より，

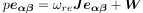...(3)

が得られます．ここで， Wは

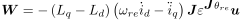
であり，線形状態方程式に収められない成分ですが，d,q軸電流の変化する過渡時のわずかな時間しか発生しないため，外乱として扱い，オブザーバを構成するときにはこれを無視します．

次に，拡張誘起電圧を推定する最小次元オブザーバを構成するために，電流微分の誤差フィードバックを行います．

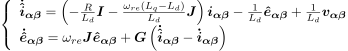...(4)

^は推定値を表しています． オブザーバでは，モデルのパラメータ誤差などが生じた場合に，推定値に誤差が残らないようにするため， このようにセンサなどにより検出可能な電流などを用いて誤差フィードバックを行います．Gはオブザーバのフィードバックゲインで，2×2の行列になります．このゲインの設定によって推定誤差の収束の速さや，外乱に対するロバスト性を考慮します．

(4)式の第1式を第2式に代入すれば，既知であるモータパラメータ(R, Ld, Lq, KE)，電圧(vαβ)，電流(iαβ)を用いて，拡張誘起電圧の推定値êαβを計算することができます．このとき，未知である速度ωreも使っていますが，一般的には電流や電圧といった電気的な変化に対して，速度の変化はゆっくりである場合が多いため，速度の推定値で代用します．また，現実的には，(4)式内の電流の微分(piαβ)を直接実行することは高周波ノイズを強調する恐れがあるため，これを避ける工夫を行い実装します．

オブザーバゲインの設計例

拡張誘起電圧モデルは，単位行列Iと交代行列Jを用いて表現されているため，Iを実部，Jを虚部に置き換え，α-β平面を複素平面に見立てることで，行列を複素数のように扱えるという特徴があります．これによって，最小次元オブザーバでは，ゲイン設計を非常に簡単に行うことができます．

ここでは，一例として極配置法による設計例を示します．まず，オブザーバの誤差方程式を導出します．オブザーバの推定誤差をε=ê-eとし，(2)式，(3)式，(4)式よりオブザーバの誤差方程式を求めると，(5)式となります．

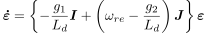...(5)

ただし，オブザーバゲインG=g1I+g2Jとします．

ここで，複素平面上におけるオブザーバの極を，-αI+βJに配置する条件を考えます．

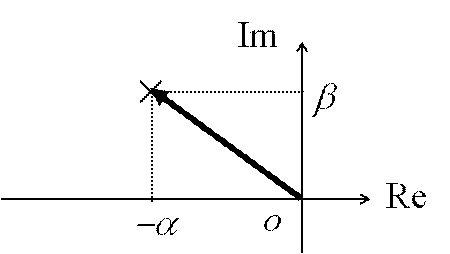
すなわち，

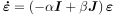...(6)

となるように，オブザーバゲインg1, g2を(7)式のように与えます．

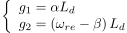...(7)

ただし，オブザーバを安定化するためには，極を左半平面に配置する必要があるため，α>0とします．

オブザーバの極α，βの設計については，以下の二点を設計指針とし，(8)式に示す極配置を与えます．

  • 速度推定誤差に対するロバスト性
  • 起電力波形の高調波外乱に対する外乱抑圧特性

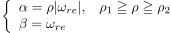...(8)

すなわち複素平面上において，原点から左に，速度のρ倍の位置に極の実軸成分αを配置し，速度に応じて比例的に移動させます．そして，虚軸成分βは速度に一致させ，αと同様，速度に応じて移動させます．αの下限値を定めるρ1，およびβの設定は，速度推定誤差に対するロバスト性に関与しており，αの上限値を定めるρ2は，高調波外乱に対する外乱抑圧特性に寄与しています．したがって，最終的には速度誤差と高調波の影響を見ながら，ρの値を調整することになります．

今回は，固定座標(α-β軸)上での例を紹介しましたが，回転座標上(d-q軸)での拡張誘起電圧オブザーバも同様に構成することができ，センサレス制御に用いられています．*[2]

全駆動域で適用可能な拡張誘起電圧オブザーバ

拡張誘起電圧オブザーバを停止・低速域まで使えるようにするするために，大沼研究室では信号重畳に適した拡張誘起電圧モデル（idモデル）*[3]を提案しています．idモデルを基にしたオブザーバも，上記に解説した一般の拡張誘起電圧オブザーバと全く同様に構成することができます．

そして，信号重畳と組み合わせる際には，オブザーバに内包しているフィルタ特性を利用して位置情報の抽出のための検波処理を行うことができます*[3}．その具体的な方法やモータパラメータ変動に対するロバスト性などについて，現在も研究を進めています．

参考文献

*[1]
Zhiqian Chen, Mutuwo Tomita, Shinji Doki, and Shigeru Okuma: "An Extended Electromotive Force Model for Sensorless Control of Interior Permanent-Magnet Synchronous Motors", IEEE Transactions on Industrial Electronics, Vol.50, No.2, April 2003, pp.288-295
*[2]
市川真士・陳志謙・冨田睦雄・道木慎二・大熊　繁：「拡張誘起電圧モデルに基づく突極型永久磁石同期モータのセンサレス制御」，電気学会論文誌D，Vol.122，No.12，pp.1088-1096, 2002
*[3]
大沼 巧*：「位置センサレス制御のための信号重畳に適した拡張誘起電圧モデルの提案」，電気学会産業応用部門大会，沖縄, 1-194, 2011.9.8
ページのトップへ戻る