拡張誘起電圧モデル - Extended Electromotive Force Model -

〜 よい制御は よいモデルから 〜

制御対象となる機械（モータ）を思い通りに動かす，すなわち制御するためには，まず制御対象の振る舞いを"モデル化"することが重要です．制御におけるモデルとは，制御対象にある入力を与えたときにどのような出力になるかを記述したもので，一般には微分方程式（状態方程式，伝達関数）などの数学により記述されます．

埋込磁石同期モータ（IPMSM）の位置センサレス制御が盛んに研究され始めた2000年前後から，拡張誘起電圧モデル（EEMF Model : Extended Electromotive Force Model）*[1]という制御モデルが提案され，実用化してきました．拡張誘起電圧モデルを用いる利点は，突極性の有る無しに関わらず，同期モータの位置情報を取り出しやすい形でモータモデルを表現できるところにあります．

d-q軸上のIPMSMの電圧方程式

一般によく知られている同期回転座標系（d-q軸）上におけるIPMSMの電圧方程式は，(1)式で表されます．（座標系の定義についてはこちらのリンクを参照）

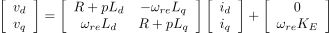...(1)

Rは抵抗，Ld,Lqはd,q軸インダクタンス，KEは誘起電圧定数，ωreは回転子の回転角速度，vd,vqはd,q軸電圧，id,iqはd,q軸電流，pは微分演算子を表します．

これを固定座標であるα-β軸に変換すると

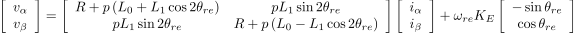(2)

ただし，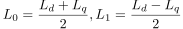

となり，この式から回転子の位置θreを求められれば，制御に必要な回転子の位置情報が推定できることになります． しかし，(2)式の中にはθreの項が，インダクタンスによる2θreの成分と永久磁石によるθreの成分に分かれており，このままでは位置を求めることが困難です．

一般の拡張誘起電圧モデル

ここで，(1)式の右辺第1項のインダクタンス行列の部分に注目します． 実は，この部分が対称になっていないために，固定座標に変換したとき，2θreの項が出てきてしまうのです． そこで，このインダクタンス行列が対称になるように，(1)式を次のように変形します．ここでは，対角成分をLd, 非対角成分をLqに統一するように式変形します．

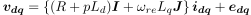...(3)

そして，(3)式の中にあるedqは，(4)式のように表されます．

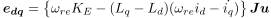...(4)

ただし，(3)式, (4)式中の太字のvdq, idq, edq, I, J, uはベクトル，もしくは行列を表しており，

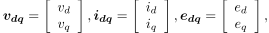
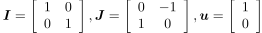
です．定義から明らかなように，Iは単位行列，Jは90度の回転行列，uはd軸方向の単位ベクトルを表しています．また，(4)式中のドットの記号・は時間微分を表しており，ドットのついた変数であるiqのみに対して微分を作用させるため，微分演算子pと区別しています．

(3), (4)式の導出においては，インダクタンス行列を対称にするためにはみ出した部分を誘起電圧の一部として捉え，永久磁石により発生する誘起電圧を拡張した形で(4)式のedqの中に集約しています．この拡張した誘起電圧であるedqを拡張誘起電圧と呼びます．

これを固定座標系に変換すると，

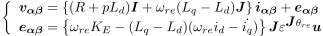...(5)

となり，確かにθreの項が一つに集約されています．

ただし，vαβ, iαβ, eαβはそれぞれ固定座標上の電圧，電流，拡張誘起電圧ベクトル，εJθreは回転行列であり，

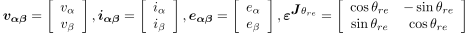
と表すことができます．

(5)式に基づいて，次に説明するオブザーバを構成し，拡張誘起電圧ベクトルeαβを推定することにより，その位相から回転子の位置を求めることができます． 固定座標系の拡張誘起電圧の各成分eα，eβから回転子位置θreを求める式は，次式となります．

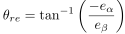...(6)

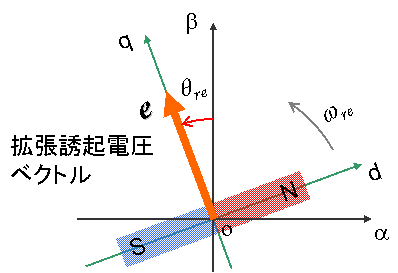
信号重畳に適した拡張誘起電圧モデル（idモデル）

一般に知られている拡張誘起電圧モデルは，(4)式，(5)式にあるように速度起電力による位置情報だけでなく，突極性（LdとLqの差，インダクタンスの位置依存性）による位置情報も含んでいます．そのため，モータの回転速度が停止・低速から中高速域まで全速度域にわたって，位置推定に利用することができます．

しかし，モデル式が示すように，低速域（ωreが小さい領域）において突極性による項を利用するためには，q軸電流の微分を生成する必要があり，q軸電流を常に変化させておく必要があります．q軸電流を変化させるためには，モータに高周波の信号電流を印加することとなり，信号電流によるトルク脈動・騒音・損失の増加，また電流制限にかかりやすくなるといったデメリットもあります．その影響は，モータの負荷となる機械系，モータ特性，信号印加条件によっても異なるため，実用的にはこれらの影響が出ないような条件を選択しつつ，位置推定の方法を工夫して制御性能を維持できるように個々に調整を行います．

これに対し大沼研究室では，中高速域における拡張誘起電圧の推定法として実績のあるオブザーバによる位置センサレス制御を，低速域に拡大することが可能となるよう，新たに"信号重畳に適した拡張誘起電圧モデル"（idモデル）*[2]を提案しています．

信号重畳に適した拡張誘起電圧モデルを用い，トルク脈動を発生させない信号重畳法を適用することで，全駆動領域にわたって拡張誘起電圧オブザーバによる位置センサレス制御が可能になります．大沼研究室では，この方法をベースにした安定で使い勝手の良い位置センサレス制御システムの確立を目指しています．

参考文献

*[1]
Zhiqian Chen, Mutuwo Tomita, Shinji Doki, and Shigeru Okuma: "An Extended Electromotive Force Model for Sensorless Control of Interior Permanent-Magnet Synchronous Motors", IEEE Transactions on Industrial Electronics, Vol.50, No.2, April 2003, pp.288-295
*[2]
大沼 巧*：「位置センサレス制御のための信号重畳に適した拡張誘起電圧モデルの提案」，電気学会産業応用部門大会，沖縄, 1-194, 2011.9.8
ページのトップへ戻る