トルク勾配に基づく非線形モータの仮想空間モデル[1]
モータは，適用範囲拡大に伴い高出力密度化が進み，磁気飽和・d-q軸間の干渉・空間高調波といった非線形特性の影響を考慮した制御系が求められています．また，極数変換・温度変化・可変磁力といった可変パラメータが前提のシステム最適化が進んできています．
このような，いわゆる「非線形モータ」に対しては，限られたモータパラメータを用いた線形近似モデルに基づく制御の限界を感じることも多くなっています．
そこで，本研究では，このような非線形性の強いモータに対し，高精度なトルクマップデータを用いてトルク制御性を向上させる新しい制御モデルの提案をしています．
（著者：大沼 巧. 2023.3.18）
トルクマップ
モータのトルクτは，d,q軸電流id,iqの関数となっており，τ(id,iq)のように2変数関数として表すことができます．下図のように，id,iqを直交座標軸にとり，トルクを電流空間上のコンター図で表したものをトルクマップと呼びます．
ここでは，2次元電流平面上のマップとしていますが，空間高調波などを考慮する場合には，回転子の磁極位置θrも変数とし，τ(id,iq,θr,...)のように多次元のマップとして拡張することもできます．
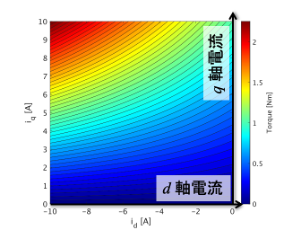
トルクの勾配と仮想磁束
トルクの勾配∇τ（grad τ）は式(1)のように定義できます．d軸方向の成分はτをidで偏微分したもの，q軸方向の成分はτをiqで偏微分したものです．∇τはベクトル量となるため，図のような矢印で表現することができます．矢印の向きは，各点における定トルク曲線の法線方向であり，矢印の長さは，定トルク曲線の粗密を表しています．
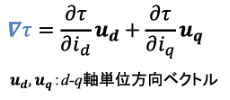...(1)
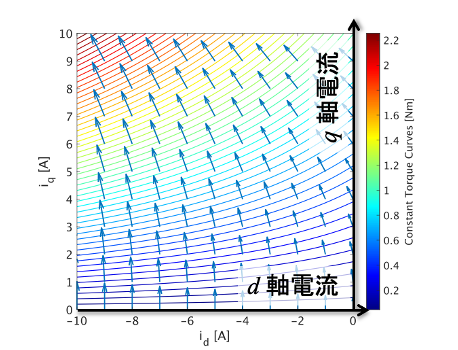
トルク勾配∇τは，式(1)の定義からわかるように，トルクを電流で割っているため，磁束の単位を持っています．そこで，トルク勾配∇τを90度回転させたものを仮想磁束Ψmとします．そして，これらを正規化し，基底ベクトルut，ufを作ります．このようにすることで，トルク勾配と仮想磁束を元に，最大トルク制御座標系f-t軸を定義することができます．
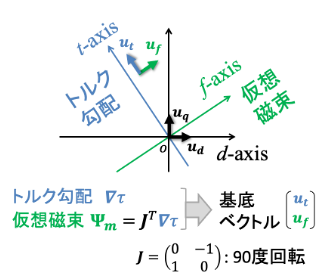
最大トルク制御座標上の電流空間
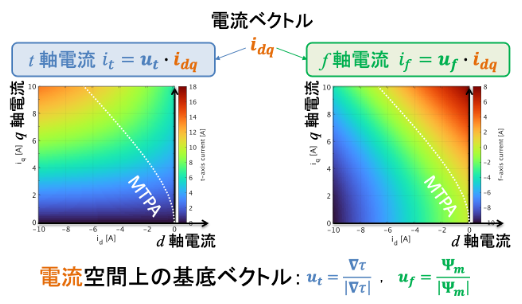
最大トルク制御座標上の電流空間は，電流ベクトルidqに対して，ut，ufとの内積をとることによって作れます．電流空間上の基底ベクトルというのは，utがトルク勾配，ufが仮想磁束をそれぞれ正規化した単位方向ベクトルです．
下図は，横軸にd軸電流，縦軸にq軸電流をとり，それぞれt軸電流，f軸電流をカラーマップで表した例です．右の図から分かるように，f軸電流ifが0AのところがMTPA（最大トルク/電流制御）のラインに重なっており，MTPAが達成されるときif=0ということが確認できます．
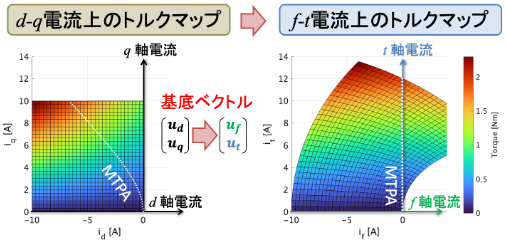
トルクマップの写像
f-t座標系へトルクマップを写像すると，図のように平面を右方向へ引き延ばした変形をしていることになります．if-itの空間でトルクマップを見ると，t軸上にMTPAラインが重なっていることがわかります．
このように，トルク制御に適した状態空間へ，電流・電圧を変換できるということが，仮想空間モデルの特長です．
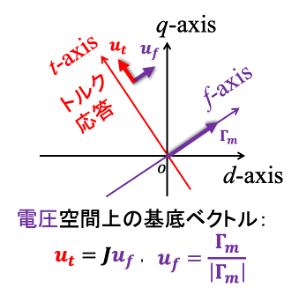
電圧空間における最大トルク制御座標系
次に，最大トルク制御座標系を電圧空間上で考えてみます．まず，d-q軸上の電圧を，定常項のv0と過渡項のv1という二つの成分に分けます．そして，この過渡項v1の成分が，電流の時間微分によって生ずるというインダクタンスモデルで考えます．
...(2)
そうすると，トルクの時間微分dτ/dtを，トルク勾配と電流微分の内積で表現することができ，さらに仮想磁束Ψmと過渡電圧v1を使って変形していくと，式(3)のようになります．
...(3)
ここで，Γmは，式(4)のように仮想磁束Ψmをインダクタンス行列で変換したものです．
...(4)
式(3)のように，トルクの時間微分がJΓmとv1の内積によって表現できるということは，Γmとその直交ベクトルを基準に，電圧空間上にt軸，f軸を定義すると，トルク応答にはt軸電圧のみが有効であるということがいえます．
トルク制御系への適用例
この仮想空間モデルを用いたトルクフィードバック制御系の例を文献[1]にて発表しています．
本研究では，引き続き，この仮想空間モデルを用いて，非線形モータのトルク制御性の向上を目指しています．
参考文献
- *[1]
- 大沼 巧：「トルクマップの勾配に基づく非線形モータの仮想空間モデル」，電気学会全国大会, 5-112(2023)
