様々な特徴を持つコンピュータ言語の中で,Mathematicaは,
- インタープリタ方式のため,会話形式で効率良く答えを導くことが出来る
- 一つ一つの命令が強力であり応用範囲が広い
- 数式処理が出来る
- 強力なグラフィック能力を持っており,計算結果を簡単にグラフ化出来る
実験では,Matehmaticaの基礎を学び, 電気・電子工学上の簡単な問題を解けるようにする。
- 沼津高専計算機センターで Matehmatica を使う時の注意点は, ここに記述されています。
- 他にも,MS-Windows 上のソフトウエアとしても存在する
(MS-Windowsアプリの場合,右上[×]の終了ボタンで終了することも可能)
- ウインドウ内に普通に数式を打ち込むことができる。
但し,Matehmatica固有の書式が有るので注意すること- "入力が完了した。今から計算させたい"というときは,(Shift)+(Enter) を押す
- (Enter)は,複数行の入力の時に各行を区切るために使用
- 掛け算は スペースで表わされる
例: "k 5" とは,k と 5 を掛け算することである。
まちがい:"k5"と隙間なく書くと,k5 という変数とみなされる - 組み込み関数は,大文字から始まる。また,
引数を囲むカッコはカギカッコ"[","]" が使われる。
なお,普通の数式上のカッコは,普通のカッコが使われる
例: "(Sin[ x ] + 2) / 3" - 習慣的に,ユーザが定義する名前(変数とユーザー定義関数)は
総て小文字が使われる
例: "i, a, menseki, myfunc" - 一度計算させる時に使った入力部分は再利用が可能です。 マウスを使って元に戻って入力をやり直すと, キー入力が簡単です。(前の結果は消えてしまうけど)
※ 囲まれた部分は Mathematica のウインドウ内の情報であり, 太文字部分はユーザの入力部分, 赤色の文字は筆者が後で書き込んだコメントである。
※ Mathematica は,何回目の入力なのかを自動的に表示してくれる。 特に計算結果と関係しないので,その値にこだわる必要はない
(足し算) In[1]:= 3+4 Out[1]:= 7 |
(掛け算,引き算,割り算) In[2]:= (11 3 - 1) / 8 Out[2]:= 4 |
(べき乗と階乗) In[3]:= 3 10^5 / 3! Out[3]:= 50000 |
In[4]:= 1 / 3 - 1 / 4 1. / 3 - 1 / 4 Out[4]:= Out[5]:= (自分で入力して確認してみよう) |
入力行の数だけ答えが返ってきます。
※ 整数を入力すると分数演算をし,誤差無しで評価します。
※ 小数点のある数値を一つでも含む演算は,数値計算になります。 特に指定しない時は,パソコンのハードウエアの精度で演算します。
In[6]:= N[1 / 3 - 1 / 4 , 20] (自分で入力して確認してみよう) |
In[7]:= N[Pi,50] (円周率 π) N[E,50] (自然数 e) I ^ 2 (複素数 i) (1 + I) ^ 2 (複素数 i) Sqrt[2] (ルート) Sin[Pi] (正弦関数。他に Cos[ ], Tan[ ] など) Exp[2] (指数関数。他に Log[ ], Log[a,x](a底のログ)など) Re[ 1 + 2 I] (実数部。他に Im[ ](虚部),Abs[ ]絶対値など) (自分で入力して確認してみよう) |
In[1]:= a=3 4 (a という変数に代入) Out[1]:= 12 (答えを表示。a という変数の表わすところです) |
In[2]:=
b=x + y
c=2 b; (";" を最後に付加)
d=3 x + c
(自分で入力して確認してみよう)
|
※ 数式処理が出来るため,未知数 x を x のまま置いて計算してくれます。
In[4]:= c Out[4]:= 2 (x + y) |
In[5]:= % Out[5]:= 2 (x + y) |
ちなみに,%% は二つ前の,%%% は3つ前の,n個の % は n個前の計算結果
In[6]:= z=Out[1] Out[6]:= 12 |
In[7]:= ?Sin (自分で入力して確認してみよう) |
なお,??キーワード とすると,詳細な情報を見ることが出来ます
また,?Si* というふうに"*"を使うと,Si で始まる全ての単語を,
?*in* というふうに"*"で挟むと,in という文字を含む全ての単語を出力します
In[1]:=
f1=x; (一次式)
Plot[f1,{x,-4,4}]
(縦軸 f,横軸 t でグラフを書く)
(縦軸の目盛は自動)
(横軸は x が -4 から 4 まで変化)
(自分で入力して確認してみよう)
|
In[2]:=
f1=x; (一次式)
f3=- x^3/6; (f3は3次式)
Plot[{f1 , f1 + f3 , Sin[x]},{x,-4,4}]
(複数の関数を同時にプロットするには,
"{"と"}"で括って","で区切れば良い)
(自分で入力して確認してみよう)
|
In[3]:=
y1=Sin[t]; (正弦波)
y3=Sin[3 t] / 3; (振幅と周期の異なる正弦波)
Plot[{y1,y3,y1+y3},{t,0,2 Pi}]
(自分で入力して確認してみよう)
|
- 例 : y = Sin[x] Cos[x], x が -π から +π まで変化
- 例 : y = Exp[x/2] sin[3 x], x が -π から +π まで変化
- 例 : y = x ^ 2 + 2 x + 1, x が -2 から +2 まで変化
- ☆レポート課題☆
上記 In[2]の入力に加えて,
f5= x^5/5! ,
f7=-x^7/7! ,
f9= x^9/9! ,
f11=-x^11/11! ,
f13= x^13/13! ,
(以下同様)
を加えて行くと正弦波に収束するという。自分で確認してみよう!! - ☆レポート課題☆
上記 In[3]の入力に加えて,
y5=Sin[5 t]/5 ,
y7=Sin[7 t]/7 ,
y9=Sin[9 t]/9 ,
y11=Sin[11 t]/11 ,
(以下同様)
を加えて行くと方形波に収束するという。自分で確認してみよう!! - 他にも自分で関数を考えてトライしよう
参考:Mathematicaの文法について
In[5]:=
y=Cos[50t]; Plot[y
,{t,0,2 Pi}
]
(自分で入力して確認してみよう)
|
※ 適当な場所で区切ることにより,一つの式を複数行で書くことも出来る
参考:プロット関数を使いこなす足がかり
In[6]:=
y=Cos[50t];
Plot[y,{t,0,2 Pi}
,PlotDivision->100
,PlotRange->{{0,8},{-2,2}}
,Frame->True
,GridLines->Automatic
]
(色違い部分はどれでも幾つでも入力可)
(自分で入力して確認してみよう)
|
※ 上記の色違い部分は,どれでも幾らでも付け加えられます。
※ PlotDivisionはどれだけ細かく範囲を切って計算するかを指定します。 特に指定が無い時は 20 が与えられています。 上記の Cos[50t] のように変化が激しい関数の場合, これを指定しないと正しい形が表示されないことが有ります。
※ PlotRangeはグラフの表示範囲のことです。{{xmin,smax},{ymin,ymax}}。
※ Frameは外枠のことです。
※ GridLinesは格子のことです。
※ 他にも様々な指定が出来ます。 ??Plot と入力してマニュアルを見てみよう
参考:レポート課題のヒントとして-1
In[7]:=
y=Series[Sin[x],{x,0,11}]//Normal
(自分で入力して確認してみよう)
|
- 上の例では,Sin[x]という関数を,
- 変数 x に関して級数展開する。
- x=0 という値を中心として。
- 次数は,x^11 オーダーまで。
- 後ろに //Normal をつけたことにより,x^12 オーダーを越える誤差を無視する。
参考:レポート課題のヒントとして-2
In[8]:=
y=x;
Do[
m=2n+1;
y = y + (-1)^n x^m / m!
,{n,1,3}]
y (yの表示)
Plot[{y,Sin[x]},{x,-4,4}]
(自分で入力して確認してみよう)
|
※ Do は繰返し計算をします。この場合は n=1 から始めて n=3 まで,3回ループします。 ??Do と入力してマニュアルを見てみよう
In[1]:=
r=300; eru=1; f=50; v=141;
w=2 Pi f;
zr=r; zx=I w eru;
vin=v Exp[I w t];
vr= vin zr/(zr+zx);
vx= vin zx/(zr+zx);
Plot[{Re[vin],Re[vr],Re[vx]}
,{t,0,0.05}
,PlotStyle->{Thickness[0.005],Thickness[0.01],Thickness[0.02]}
]
(自分で入力して確認してみよう)
・300[Ω] と 1[H]の直列,50[Hz] 141[V]の電源
・w とは ωのこと
・zr, zx は,各部のインピーダンス。コイルには虚数がくっつく
・各部の電圧は,Expを使って表現。実際の値は,Real部分を見れば良い
・Expの実部を取り出してグラフ化
・Thicknessにて,太さの異なる3本のグラフとした
|
In[2]:=
r=300; c=10 10^-6; f=50; v=141;
w=2 Pi f;
zr=r; zx=1 /(I w c);
vin=v Exp[I w t];
vr= vin zr/(zr+zx);
vx= vin zx/(zr+zx);
Plot[{Re[vin],Re[vr],Re[vx]}
,{t,0,0.05}
,PlotStyle->{Thickness[0.005],Thickness[0.01],Thickness[0.02]}
]
(自分で入力して確認してみよう)
・300[Ω] と 10[μF]の直列
・コンデンサには虚数がくっつく
・他は,コイルとのかいろと同一
|
(ライブラリの読み込み)
In[1]:=
<<Graphics`Graphics`
(区切り記号に注意: " や ' でなく ` です))
In[2]:=
LogPlot[ {x ^ 2, x ^ 5}, {x, 0, 5}];
LogLogPlot[ {100 ^ x, 10 ^ x}, {x, 1, 100}];
(片対数,両対数グラフ)
(自分で入力して確認してみよう)
|
※ いったん読み込めば,後は電源を切るまでその機能を使うことが可能。
※ これ以外にも様々なライブラリが有るので,時間が有ったら調べてみよう
In[3]:=
LogLogPlot[ 50/Sqrt[1 + (2 Pi f / 1000) ^2 ], {f, 1, 10^6}];
Plot[ Log[10, 50/Sqrt[1 + (2 Pi 10^a / 1000) ^2 ] ], {a, 0, 6}];
(自分で入力して確認してみよう)
・いずれのグラフも,電気回路の特性を,logでグラフ化
・1行目は,LogLogPlotを使用
・2行目は,両対数グラフをPlotで実現
|
※ どちら使っても,同じ答えですが,
LogLogPlot のほうが目盛りはきれいですが,グラフにぎこちないところが有り,
Plot のほうは目盛りは対数のままですが,グラフはきれいです。(こちらが,望月のお勧め)
In[1]:=
z=Cos[x] Cos[y]
Plot3D[z,{x,0,2Pi},{y,0,3Pi}
,PlotPoints->30
,Mesh->False
,ViewPoint->{1,1,1}
]
(縦軸 z,変域 x,y で3次元グラフを書く)
x軸は t が 0 から 2π まで変化
y軸は t が 0 から 3π まで変化
色違い部分は好みで)
(自分で入力して確認してみよう)
|
※ Meshはメッシュをいれるかどうか
参考:3Dグラフで同時に2つ以上の関数を書く方法
In[2]:=
z=Cos[x] Cos[y]
fig1=Plot3D[z,{x,0,2Pi},{y,0,3Pi}]
z2=0.1 y - 0.1 x
fig2=Plot3D[z2,{x,0,2Pi},{y,0,3Pi}]
Show[fig1,fig2]
(自分で入力して確認してみよう)
|
※ Show により,2つのグラフを一つにまとめる
課題:自分で関数を考えて色々な関数をプロットして,その関数の形を確認しよう
- 正弦波の進行波
※ <<Graphics`Animation` により, Graphicsライブラリの中の"アニメーション"機能を読み込む。In[1]:= <<Graphics`Animation` (ライブラリの読み込み) In[2]:= w=2Pi; k=2Pi; Animate[ Plot[Sin[w t - k x],{x,-1,2}] ,{t,0,2,.1} ] (アニメーション(連続で画面を描画)) (自分で入力して確認してみよう)
課題:自分で関数を考えて色々な関数をプロットして,その関数の形を確認しよう
以下,先人達の作った面白いプログラムを紹介する。 これらプログラムの中の関数については,分からないことは, ??<name> 等を使って自分で調べよう
- 円弧の回転(鴫谷君作)
In[3]:= Animate[ ParametricPlot[ {Cos[x+t],Sin[x+t]} ,{x,0,Pi/12} ,PlotRange->{{-1,1},{-1,1}} ,AspectRatio->Automatic ] ,{t,0,2Pi-Pi/12,Pi/12} ] (自分で入力して確認してみよう)
- 球のらせん運動(木内君作)
In[4]:= Animate[ ParametricPlot3D[ {Cos[t] Cos[u] + Sin[v] ,Sin[t] Cos[u] + Cos[v] ,Sin[u]+v/3} ,{t,0,2Pi} ,{u,-Pi/2,Pi/2} ,PlotRange->{{-2,2},{-2,2},{-1,6}} ] ,{v,0,15,0.5} ] (自分で入力して確認してみよう)(もし,上のプログラムで動かないなら,こちらだけでもトライしてみよう。) v=0; ParametricPlot3D[ {Cos[t] Cos[u] + Sin[v] ,Sin[t] Cos[u] + Cos[v] ,Sin[u]+v/3} ,{t,0,2Pi} ,{u,-Pi/2,Pi/2} ,PlotRange->{{-2,2},{-2,2},{-1,6}} ] (自分で入力して確認してみよう)
- リサージュ図形(高柳君作)
In[5]:= Animate[ ParametricPlot[ {Cos[3x-t],Sin[5x-t]} ,{x,0,2Pi} ] ,{t,0,2Pi-Pi/18,Pi/18} ] (自分で入力して確認してみよう)
- らせん模様の回転(加藤賢作)
In[6]:= Animate[ ParametricPlot[ {t Cos[s+t],t Sin[s+t]} ,{t,0,4Pi} ,PlotRange->{{-4Pi,4Pi},{-4Pi,4Pi}} ,AspectRatio->Automatic ] ,{s,0,2Pi-Pi/12,Pi/12} ] (自分で入力して確認してみよう)
自分で打ち込んで確認しよう
In[1]:= a=1 + x (a という変数に代入) Out[1]:= 1 + x (答えを表示。a という変数の表わすところです) |
In[2]:= b=a^2 + 1 + x Simplify[b] Expand[b] Factor[b] (自分で入力して確認してみよう) |
※ Expand は,展開です。
※ Factor は,因数分解です。
In[6]:= c=1/(1-1/(1-x)) Together[c] Numerator[c] Denominator[c] (自分で入力して確認してみよう) |
※ Numerator は,分子を取り出します
※ Denominator は,分母を取り出します
In[10]:=
f=Sin[x]^3
f2=D[f,x]
f3=Integrate[f,x]
Integrate[f,{x,0,Pi/2}]
Plot[ {f, f2, f3}, {x,0,3Pi} ]
(自分で入力して確認してみよう)
|
※ Integrate[式,x] とは,式を x で不定積分
※ Integrate[式,{x,x1,x2}] とは,式を x=x1 から x2 まで定積分
課題:様々な関数を微分,積分しよう。
また,グラフ化し,もと関数と,微分,積分の関係を確認しよう
In[15]:= a=. (.-ピリオド-を代入とは,変数のクリア) In[16]:= a Out[16]:= a (aを出力。ここでは,a は a そのものです) In[17]:= b=a ^ 2 Out[18]:= 2 a (b を aの自乗と定義) In[19]:= b /. a->3 Out[19]:= 9 (注意1 : 3 の自乗は,9です) In[20]:= b /. a->4 Out[20]:= 16 (注意1 : 4 の自乗は,16です) In[21]:= b Out[22]:= 2 a (b は aの自乗のままです) In[23]:= a=2 Out[23]:= 2 (注意2 : a を 2 に固定しました) In[24]:= b Out[24]:= 4 (その結果,b=4 になりました。) In[25]:= b /. a->3 Out[25]:= 4 (注意3 : b=4 なので,aに依らず答えは 4) (自分で入力して確認してみよう) |
こういう時のために,/. と -> という演算子が用意されています。
※ 注意1: /. という演算子は, -> という演算子と組で使われます。
※※※ /. は,「置き換えよ」,という意味。
※※※ -> は,置き換える内容を指示します。
※※※ 式を評価するとき,一時的に置き換えをします。
※※※ 上の例では,a を一時的に 3 に置き換えて,a^2 を計算しています。
※ 注意2: いったん a=2 とすると,b=4 になります。( a^2 ではなくなります)
※ 注意3: b=4 になっていますから,a をどんな値にしても,b には影響しません。
| Gain = | V2 V1 |
周波数は,1 Hz から 10 MHz まで変化させることとする。
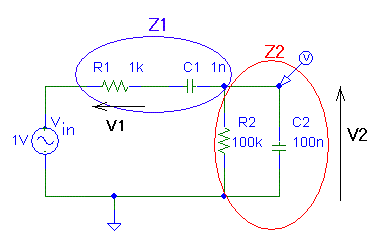
これを解くに当たって,z1,z2 という変数を,図の通り定義する。
(Mathmatica では,小文字から始まる名前だけが,ユーザーが定義できる。)
自分で打ち込んで確認しよう
In[1]:= w=.; r1=.; r2=.; c1=.; c2=.; z1 = r1 + 1/(I w c1) z2 = 1/( 1/r2 + I w c2) gain1 = ( z1 / (z1+z2) ) ( r1 / z1 ) gain2 = z2 / (z1+z2) (自分で入力して確認してみよう) |
※ 1行目 : 数式処理の前には,変数のクリアが必要です。
※ w は,オメガの積もりです。似ているので,つい使いました。
※ これにより,z1 と z2 と 各gain が表示されます。
※ ただし,gain1 とは,図の v1 と vin との比です。
※ 同じく,gain2 とは,図の v2 と vin との比です。
※ 数式処理のありがたみが身にしみます。
※ 複素数...大文字の I ...を自由に使えるのも有難い!!
In[4]:= Simplify[gain1] Factor[gain1] (自分で入力して確認してみよう) |
※ ほかに,Expand 等もあります。(前出)
※ グラフ描画には不要な操作です。
In[6]:=
g=gain1/.{r1 -> 1000 ,
c1 -> 10^-9,
r2 -> 10 10^5 ,
c2 -> 100 10^-9}
Plot[20 Log[10, Abs[g]] /. w->2 Pi 10^ff ,
{ff,0,7},
PlotRange->{{0,7},{-90,10}},
GridLines->Automatic]
(自分で入力して確認してみよう)
|
※ ff の 0 〜 7 にわたる変化は,周波数 の 1 Hz 〜 10 MHz の変化になります。
※ 0 db とは 1倍, -20 db とは 0.1 倍,-40 db とは 0.01 倍です。
※ /. という演算子は, -> という演算子と組で使われる事が多いです。
※ /. は,置き換えよ,という意味。
※ -> は,具体的な置き換えを指示します。
※ 同様に gain2 の特性も書かせてみよう。
In[8]:=
Plot[ArcTan[Re[g], Im[g]] 180/Pi /. w->2 Pi 10^ff , {ff,0,7},
GridLines->Automatic]
(自分で入力して確認してみよう)
|
※ 位相の変化を表わします。
※ Re と Im は,実部と虚部を取り出す関数です。
※ 180/Pi を掛ける事により,2π ラジアンを 360度 に変換しました。
※ 同様に gain2 の特性も書かせてみよう。
In[9]:= N[ w/(2 Pi I) /. Solve[g==0,w] ,7] N[ w/(2 Pi I) /. Solve[1/g==0,w] ,7] (自分で入力して確認してみよう) |
| g = K * | f * (1 + i f / f1 ) * (1 + i f / f2 ) ... (1 + i f / fa ) * (1 + i f / fb ) ... |
※ 上記の 1 行目により,f1, f2, ... を求めます。 もしも 0 という値があれば, 最初の f という項があるということです。
※ 上記の 2 行目により,fa, fb, ... を求めます。
※ 同様に gain2 の特性も書かせてみよう。
以上を,一括してみました。一部変更しました。
In[12]:=
w=.; r1=.; r2=.; c1=.; c2=.;
z1 = r1 + 1/(I w c1)
z2 = 1/( 1/r2 + I w c2)
gain1 = ( z1 / (z1+z2) ) ( r1 / z1 )
gain2 = z2 / (z1+z2)
condrc={ r1 -> 1000 , c1 -> 10^-9,
r2 -> 10 10^5 , c2 -> 100 10^-9};
condw= w->2 Pi 10^ff;
g=gain1/.condrc;
N[ w/(2 Pi I) /. Solve[g==0,w] ,10]
N[ w/(2 Pi I) /. Solve[1/g==0,w] ,10]
Plot[{ 20 Log[10, Abs[g]] /. condw ,
ArcTan[Re[g],Im[g]]40/Pi /. condw },
{ff,0,7},
PlotRange->{{0,7},{-100,20}},
PlotStyle->{Thickness[0.005],Thickness[0.01]},
GridLines->Automatic]
g=gain2/.condrc;
N[ w/(2 Pi I) /. Solve[g==0,w] ,10]
N[ w/(2 Pi I) /. Solve[1/g==0,w] ,10]
Plot[{ 20 Log[10, Abs[g]] /. condw ,
ArcTan[Re[g],Im[g]]40/Pi /. condw } ,
{ff,0,7},
PlotRange->{{0,7},{-100,20}},
PlotStyle->{Thickness[0.005],Thickness[0.01]},
GridLines->Automatic]
(自分で入力して確認してみよう)
|
※ ただし,図の見易さを考慮し,位相 π を 40 としました。
課題:こうして得られた特性を,もう一度物理的に考察しよう。
更に,抵抗やコンデンサの値を変えて周波数応答を見よう。
例 ( r1 = 10 10^3 , c1 = 10 10^-9, r2 = 10^3 , c2 = 10^-9 )
例 ( r1 = 10 10^3 , c1 = 10^-9, r2 = 10^3 , c2 = 10 10^-9 )
良く見る間違いへのコメント : コンデンサのインピーダンスは,z = 1/(I w c) です。これは回路理論より明白です。 しかし実際には以下のような間違い例を良く見ます。 ちょっと考えれば判ることです。間違いに注意しましょう。
[NG : z = 1/ I w c ... 努力賞!! これをコンピュータは w c / I と解釈します ] , [NG : z = I w c ... 混乱賞!! もしもコイルならこれで良かったのですが] , [NG : z = c ... 論外!! これは,r と c のディメンジョンを混同しています]
これ以外の回路についても式を作り直して周波数応答を見よう。
(参考:夏休みの友...E3の暑い夏休み)
☆レポート課題:以下の回路について:
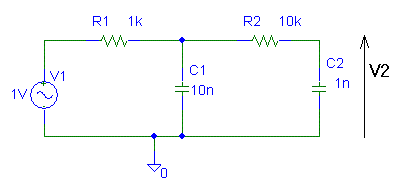
gain=v1/v2 をMathematicaで解き, また,下記の三つの定数の組について特性をグラフで書くとともに, 自ら手計算で解いてグラフ化し,Mathematicaの結果と自分の手計算の結果を比較せよ。
定数1 ( 回路図にあるもの )
定数2 ( r1 = 10^3 , c1 = 10^-9, r2 = 100 10^3 , c2 = 10 10^-9 )
定数3 ( r1 = 10 10^3 , c1 = 10^-9, r2 = 10^3 , c2 = 100 10^-9 )
- Mathematica - a System for Doing Mathematics by Computer - Second Edition (日本語版), スティーブン ウルフラム, アジソン・ウエスレイ, 1992年
- Mathematica V 2.2.3 のヘルプ画面
- 沼津高専電気工学科学生実験指導書 「数式処理-1」青木
- 沼津高専電気工学科学生実験指導書 「数式処理-2」青木
- 沼津高専電気工学科学生実験指導書 「数式処理」西村
- 沼津高専電気工学科学生実験指導書 「数式処理a,b」加藤賢一
- 例題で学ぶMathematica[数学編], 白石修二, 森北出版, 1995年
- 例題で学ぶMathematica[グラフィックス編], 白石修二, 森北出版, 1996年
- Mathematicaビギナーズガイド, T.W.グレイ J.グリン 著 榊原進 訳, (株)トッパン, 1992年