ただし,
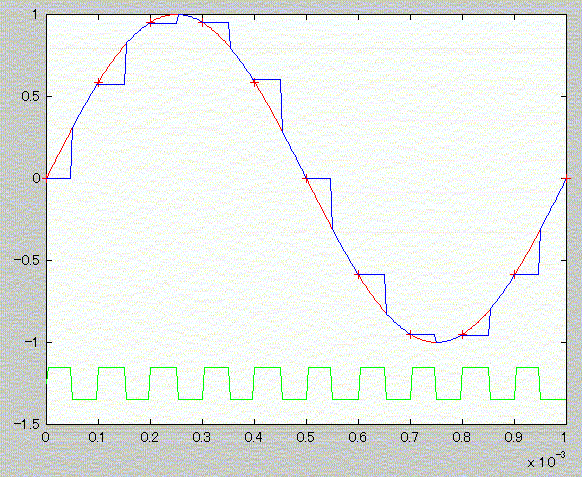
緑 = スイッチの開閉(H=Close, L=Open) ← HLと開閉の対応に注意
赤 = Vin
青 = Vout
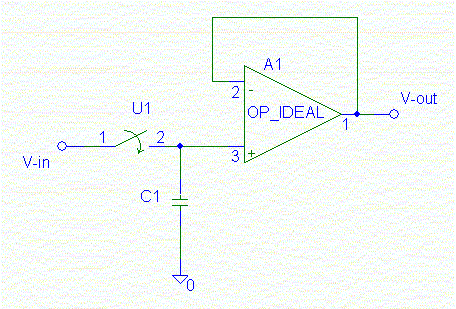
この実験では,スイッチトキャパシタ回路を使う上でキーデバイスとなる 「アナログスイッチ」という素子の特性を知ると共に, 「アナログスイッチ」を使う上で遭遇しがちなエラーである, 「エイリアシング」について学びます。
|
--- 電圧波形 --- ただし, 緑 = スイッチの開閉(H=Close, L=Open) ← HLと開閉の対応に注意 赤 = Vin 青 = Vout  |
|
| |
--- スイッチ 閉じる(Close) ---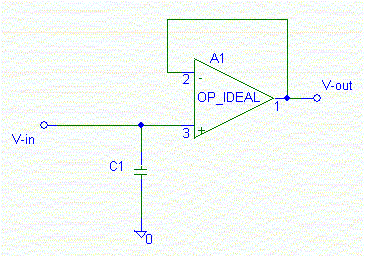 |
--- スイッチ 開く(Open) ---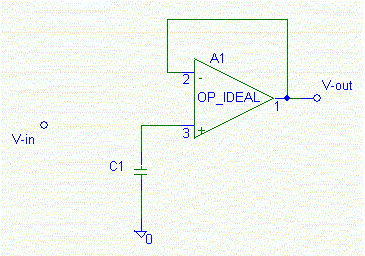 |
| m-ファイル(望月のパソコン上ではファイル名="e591.m") |
|---|
clear fs1=1000;%% [Hz] frequency of signal - 1 fs2=3000;%% [Hz] frequency of signal - 2 fc=20000;%% [1/s] sampling rate t9=0.001;%% [s] time area ph0=0;%% [degree] initial phase ddt=1/fc; [m, mi]=max([fs1 fs2]); fca=m*30; dt=1/fca; ph0rad=ph0*pi/180; %%% analog (or sample very high speed) %%% it=(0:t9*fca); ta=it*dt; y1a=sin(2*pi*fs1*ta+ph0rad); y2a=sin(2*pi*fs2*ta+ph0rad); %%% digital %%% n=(0:t9*fc); td=n*ddt; y1d=sin(2*pi*fs1*td+ph0rad); y2d=sin(2*pi*fs2*td+ph0rad); %%% subplot(2,1,1) plot(ta,y1a,'r',ta,y2a,'b', td,y1d,'r+',td,y2d,'ro') subplot(2,1,2) plot(td,y1d,'r+',td,y2d,'ro') |
上記プログラムの実行例 コメント
|