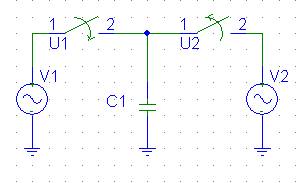
(a)スイッチトキャパシタ

(b)通常の抵抗
図1
| ir =ΔQ/TS =Cr (V1−V2)/TS | (1) |
| Req =(V1−V2)/ ir = 1/(Cr fS ) | (2) |
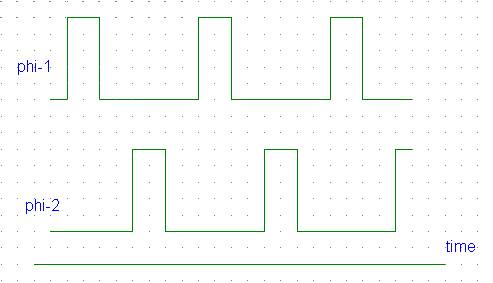
実際の回路では, スイッチはMOS電界効果トランジスタ(MOSFET)で構成される。 一例としてMOSFETを用いたスイッチトキャパシタ等価抵抗と このアナログスイッチを駆動するための2相クロック信号Φ1 , Φ2 のタイミング図を図2に示す。
Download : レポート表紙(2005.04.11)
(LastUPDATE 04/06/15 ヒントを更に充実 by 望月) (LastUPDATE 04/06/1 ヒントを充実 by 望月) (LastUPDATE 04/04/26,27 誤字脱字修正や説明文の細かいところの修正 by 望月) (Version 2.0M '98/10/14) by 望月
 (a)スイッチトキャパシタ  (b)通常の抵抗 図1 |
コンデンサとスイッチからなる図1の回路は,
次の様にAB間に接続された抵抗と等価な動作をする。
端子A,BにそれぞれV1,V2
が加えられているとする。
その時,まず切替えスイッチSがコンデンサCr
をA側に接続して
Cr の端子電圧をV1に充電する。
次にSがB側に切替わってCr
の電圧はV2になる。
この一連の動作でAからBに流れた電荷は ΔQ=Cr
(V1−V2) である。
従って,これを周期TS ごとに繰返せば,AからBに流れる平均電流は,
実際の回路では, スイッチはMOS電界効果トランジスタ(MOSFET)で構成される。 一例としてMOSFETを用いたスイッチトキャパシタ等価抵抗と このアナログスイッチを駆動するための2相クロック信号Φ1 , Φ2 のタイミング図を図2に示す。 |
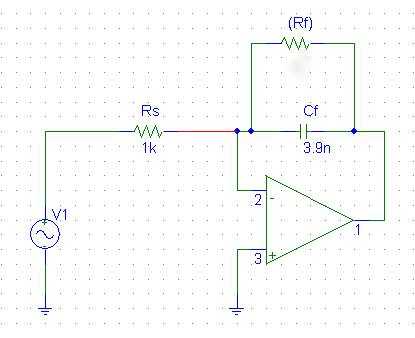
| H(jω) = fS Cr / (jωCf ) | (3) |
| 課題 | 考慮すべきこと |
|---|---|
| 課題1 周波数特性を両対数グラフに記録し, 能動RC積分回路の特性と一致する点と異なる点を指摘せよ。 |
ここでは,「指摘せよ」というだけなので,
特に考察する必要はない。 能動RC積分回路の特性と今回実験した回路の特性を同一グラフ上に示し, 両者を見比べて気づいたことを書けばよい。 なお,グラフを書くときには,意図を持って書くことが必要である。 「この実験結果は,〜の理論が正しいことを示す」 ということを結論にしたければ,同じグラフ上に, 「実験結果のプロット」と,「〜の理論による理論線」を記入し, その両者が近いかどうか議論する。 近ければ,正しいということが言える。 もし近くなければ,その実験からは〜の理論の正しさを確認できない。 (場合によっては否定してしまう) |
| 課題2 fc/2 の周波数帯において積分器として働くことを確認せよ。 |
積分回路の特性ならば,入出力特性は両対数グラフ上で右下がり45度になるはずである。
|
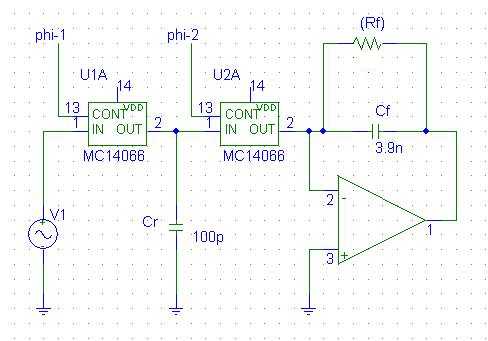
| 課題3 入力信号 Vi , クロックΦ1 , Φ2 , 容量 Cr の端子電圧, 出力信号Vo の変化の様子をタイミング図に書いて示せ。 |
入力信号 Vi ,クロックΦ1 ,
Φ2 ,容量 Cr の端子電圧,
出力信号Vo の変化の様子をタイミング図に書く時は,
労力をけちらないことである。 少なくとも回路図を3つ書き直すべきである。 3つとは次の通り: (1)Φ1 がonの時, (2)Φ1 もΦ2 もoffの時, (3)Φ2 がonの時 それらの場合場合について電流の流れ,電荷のたまり具合を見て行けば, 動作が自ずとわかるであろう。 なお,ここでは抵抗 RF は無視して (無限大であると考えて)けっこうです。 このタイミング図を描くことにより, サンプル&ホールド回路がそのまま存在していない回路なのに, 離散時間処理が行われることがわかるはず。 |
| 課題4 グラフ中に極大点,極小点があったならば,その周波数を表にせよ。 周波数 f の時の入出力特性 |Vo /Vi | と同じ大きさの入出力特性をもつ周波数は何 Hz か。 f =1kHz はどんな周波数か。 |
能動RC回路には最大点はないのだから,
この課題で問題にしているのは「能動RC回路と異なる点」である。
それを表す理論は何だったか,先週の実験を思い出そう。
思い出すべきは「用語」だけではなく,「その意味」である。
極大値と一致するものはなんだろうか。 さて,ここで「極大」等を問うているが, 「実験的に見られた最大点」を「極大」とするようでは2流である。 今回使用するファンクションジェネレータは周波数は3桁しか指定できない。 しかし,もっと実験の環境がよければ,4桁,5桁まで指定できる ファンクションジェネレータを使える可能性がある。 しかし,現状でも,グラフをプロットしながら想像力を働かせば, 極大をもたらす周波数を,求めることが出来るはずである。 |
| 課題5 fc/2 よりも高い周波数の回路動作説明せよ。 |
DC〜fc/2 の周波数帯に関する入出力特性が既に求まっているのであれば,
前回の学生実験の知識(=離散時間処理回路の理論)によって,
fc/2 よりも高い周波数における入出力特性は予想できる。
|
| 課題6 図3(b)の回路の抵抗 RF (大きな抵抗:1MΩ程度以上) を接続してある。その理由を説明せよ。 | RF については,もしもop-ampにオフセット電圧があったとき, 非常に長い時間の後で出力電圧がどうなるか考えてみれば, 答えが見つかると思います。 |
以上.