back to upper page

学生実験 指導書 E3 実験395

「演算増幅器の使い方」

'98 11/19 小変更
'98 10/15 by 望月

I. 目的
☆ここで，回路を習得するとあるが，望月は"習得"について次のように考えています。
「習得したとは，回路図を見ただけで，回路の真の動作がわかるということである。 習得した学生には，作った回路の特性を測定したり， シミュレーションして出てきた結果は，予想通りのものとなる。」
従って，回路の動作を理解することが非常に重要になります。

II. はじめに

演算増幅器は， もともとアナログ電子計算機に用いられていた高利得の増幅器で， 加減算，微積分，その他の演算に用いられていた。 集積回路技術の進歩と共に，演算増幅器も集積回路され， 一般の回路に用いられるようになった。 演算増幅器を用いることにより， 増幅回路を始め種々の演算回路を容易にしかも高性能に実現することが出来る。 時には個別部品（トランジスタやダイオード単体） を組み合わせて回路を設計するよりも， 簡単でかつ特性の優れた回路が得られる。

本実験では，演算増幅器の原理,基本的な使い方， 及びいくつかの応用回路を習得する。

III. 原理と基本回路の動作

(1)原理

演算増幅器(Operational Amplifier, op-amp)の回路記号を図１に示す。 −(マイナス)で示される反転入力端子と， ＋(プラス)で示される正相入力端子(または非反転入力端子) の二つの入力端子に加えられた電位差を増幅し， 出力端子に出力する働きをする。

図１に示すように，入力電圧 ｖ1 ，ｖ2 を加えると，出力電圧 ｖo は

ｖo ＝ Ａd *（ｖ１ − ｖ２） (1)

となる。この時， Ａd を差動利得という。

演算増幅器として要求される理想的な特性と， 実際の演算増幅器の特性の比較を表１に示す。 表からわかるように，実際の演算増幅器はほとんど理想に近い特性である。 そのため，演算増幅回路を含む回路を解析する時には， 理想特性を示す素子と仮定してもよい。

表１ 演算増幅器の理想特性と，実際の特性
パラメータ 理想特性 μＡ７４１ ＬＦ３５６
差動利得 Ａd ∞ １００ [dB] 以上 １００ [dB] 以上
入力インピーダンス ∞ ２ [ＭΩ] １０6 [ＭΩ]
出力インピーダンス ０ ５０ [Ω] ５０ [Ω]
帯域幅(−３ [dB]） ∞ １０ [Hz] １０ [Hz]

(2)演算増幅器の基本的使い方（比較器と増幅器）

演算増幅器には，大きく分けて二つの使い方がある。 一つは比較器でもう一つは増幅器である。

1. 比較器

比較器（コンパレータ）の回路例を図２に示す。 入力 ｖ１，ｖ２ にある電圧を加えた時の出力電圧を表２に示す。 前述の式(1)より，理想出力特性が計算した． しかし，演算増幅器は電源電圧よりも高い電圧は出力できないため， 実際には，＋１５ [V] または −１５ [V] の電圧しか出力しない． 従って，出力電圧には，二つの入力電圧のどちらの電圧が高いか，という情報しか出力されないことになる． 比較器は，アナログ信号をデジタル信号に変換する回路， または，デジタル信号伝送回路の受信部で用いられる．

表２ 比較器（図２の回路）の入力出力条件
入力条件 理想出力電圧 実際の出力電圧 *
ｖ１ ＞ ｖ２ ＋∞ [V] ＋１５ [V]
ｖ１ ＜ ｖ２ −∞ [V] −１５ [V]
例えば，ｖ１=１[V]，ｖ２=２[V] −∞ [V] −１５ [V]
* : 演算増幅器に加える電源電圧を ±１５[V]とする
2. 増幅器

図３の回路を，反転増幅器と呼ぶ。 この回路では，入力信号が増幅され，出力端子から出力される。 出力電圧は，基本的には電源電圧よりも小さな電圧となり， ±１５ [V] に飽和することはない。 出力端子電圧の絶対値が電源電圧よりも小さいということは， op-ampの差動入力端子と同相入力端子の電位が等しいということである， 何故なら，両者に少しでも電位差があれば，式(1)より， 出力の絶対値は無限大になるからである。 このことを逆にいうならば， 「演算増幅器により増幅器を構成する時は， 差動入力端子と同相入力端子に電位差が生じない様に設計する」 ということになる。 そのためには，図３のように出力端子の電圧が マイナス入力の端子に接続されれば良い。 この配線方法は「負帰還」と名づけられている。 表３に，図３の回路にノイズが入った場合の負帰還のある回路の動作を示す。 ノイズが入った時， 回路内でつじつまを合わせ， 差動入力端子と同相入力端子の電位差がゼロになることがわかる。

表３ 負帰還増幅回路の原理
回路の状態 入力電圧 出力電圧 正相入力端子の電圧v1 反転入力の電圧v2
初期状態 vin(固定) vout v1は常に0[V] v2=v1(=0[V])
仮定 voutにノイズが入り，
電圧上昇
経過１ voutの上昇に伴い，
v2は上昇
経過２ v2の電圧上昇に伴い，
voutは電圧下降
結果 voutはもとの電圧に戻る。 v2は元の電圧に戻る。
注: この回路では v2 はアースに接続されていないにもかかわらず， その電位は常に v1 と同じ電位（即ち 0[V]）である。 この様なことを， 仮想ショート（Virtual or Imaginary short） または仮想接地（Virtual or Imaginary ground）されたという。

IV. 回路，実験手順，課題

op-ampを使った回路を説明すると共に， 実験手順と，実験の課題を述べる。

共通課題

以下に上げる回路について， 理論的に動作を求めると共に， 実際に，または，コンピュータ上で回路を組み，それを動作させて， 各部の信号を観察し， 設計通りに動いているか確認すること。 （場合によってはグラフに記入等，適宜記録法を考えること）
☆レポートの効率的な書き方の例をこっそり(!?)教えます。
  • それは，この電気工学科の演習室で，ワープロを使ってレポートを書くことです。
  • サーバコンピュータ"FARAD"上にあるアカウント名と同じ名称のディレクトリは， 学生がファイルを専用に保管できる領域ですから， もしも作業が明日以降にずれ込んでも安心です。
  • Windows上のソフトウエアで共通的に使うことのできる「コピー & ペースト」 機能を使うことにより，指導書を写す手間が大幅に楽になります。
  • ソフトウエアを動かすことによって得られた画像は， 次の操作でワープロ上に貼り付けることが可能です。
    1. 前提条件の確認：ワープロも， 画像を取り込みたいソフトウエアも立ち上っている。
    2. 取り込みたい画像が表示されているウインドウを，アクティブにします。 (マウスを持っていって，作業と関係の無いところをクリックすれば良い)
    3. 「Alt」キーを押し始めます。
    4. 「Print Screen Sys Rq.」というキーを押します。
    5. 「Alt」キーを放します。
    6. ワープロのウインドウを，アクティブにします。
    7. 画像を張り込みたいところをマウスでクリックします。
    8. 「編集」メニューから「張り付け」を選択します。
    重要:画像の数は最小限に減らし， それぞれも波形が分かる範囲でなるべく小さくしよう。 ←画像はべた画面になるため， 印刷のインクが異常に減る原因になります。
  • この演習室にはプリンタもありますから，ここで出力できます。
  • フロッピーディスクを持っていて，家に同じワープロがある人は， 自宅で作業を続けられます。 (注意：もしも同じワープロだがバージョンが古いという場合は， この部屋でセーブする時に「ファイル名を指定して保管」 というメニューを選び， その際にファイル形式として古いバージョンを指定しよう。
  • もしもここに今表示されているところを全部コピーしてワープロするならば， 「必要なところを取捨選択する」 ように。 この文章には，ここのコラムなどレポートに不要な部分があります。 「ふさわしくない部分が残されたレポート」 が減点対象になることは言うまでもありません。

実験1-実験で

実験室での反転増幅器の実験，については，ここでは省略します。

実験2-コンピュータを使って

準備

実験の準備のために以下の処理をして下さい。


ソフトの使用法について

ソフトは直感的に使えると思います。
以下に，質問の多かったことについて，まとめます。

(1) 比較器

次の図は比較器である。 反転入力端子と，非反転入力端子の電圧を比較し， 非反転入力端子の電位が高い時には ＋１５ [V]* の電圧が， 反転入力端子の電位が低い時には −１５ [V]* の電圧が出力される。
( * : 演算増幅器に供給される電源電圧が ±１５ [V] の時)


実行例

回路を組むときの注意
課題

(2) 反転増幅器

次に示すのは負帰還増幅回路である。 演算増幅器と抵抗 R1 と R2 によって構成されている。
この回路の電圧増幅率を計算しよう。
負帰還がかかっているため，常に仮想ショートが成り立つため， 反転入力端子の電位は，非反転入力端子の電位と同じく 0V になる。 入力電圧 e1 を与えた時， この時，抵抗 R1 を流れる電流は，

ｉR1 = (e1 - 0[V]) ／ R1 = e1 ／ R1 (2)

である。 演算増幅器の入力インピーダンスは ∞ [Ω] のため， この電流は全て抵抗 R2 を流れる。 これより，抵抗 R2 の両端に発生する電位差は，

[抵抗 R2 に発生する電圧] ＝ ｉR2 * R2 ＝ ｉR1 * R2 (3)

である。 反転入力端子の電位が ０ [V] であることと， 電流の流れの方向を考慮に入れ， 入力電圧 e1 と 出力電圧 ｖout の関係を求めるならば，式(4)が求められる。

ｖout ＝ − (R2/R1) * e1 ． (4)


実行例

回路を組むときの注意
課題

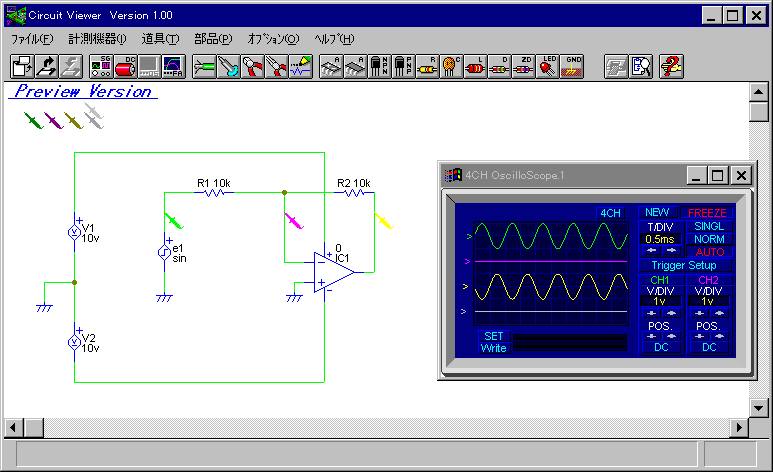
(3) 加算器

加算器の回路を次に示す。 この回路は，反転増幅器の回路を拡張したものである。 この回路でも，演算増幅器の入力インピーダンスは無限大であり， 2つの入力端子には仮想ショートが成立つことから， 出力電圧は，

ｖout ＝ − (R2 / R1) * e1− (R2 / R3) * e2 (5)

で与えられる。 もしも，入力部の２つの抵抗値が等しく，いずれも R ならば，出力電圧は，

ｖout ＝ − (R2 / R) *（e1 ＋ e2） (6)

となる．
この回路では２入力の加算器を示したが， 容易に３入力以上の加算器に応用できる。


実行例

回路を組むときの注意
課題

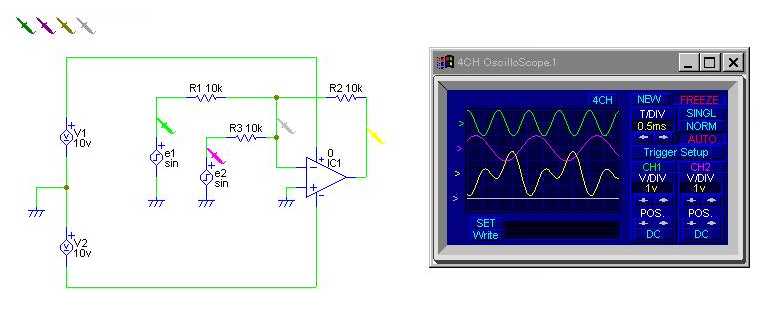
(4) 積分器

能動素子を使用しないで抵抗とコンデンサだけで積分回路を構成すると， 回路は図７のようになる。 この回路では，信号の周期が回路の時定数 τ ＝ ＲＣ よりも充分に小さくなければ出力信号に誤差が生じてしまう。 図８に破線で， この回路にステップファンクション信号が入った時の出力信号を示す。 図８に実線で，演算増幅器を使った積分器の出力信号を示す。 このとき，回路は図９である。 この回路でも負帰還の働きで仮想ショートが成立つため， 反転入力端子の電位は 0[V] である。
この時，抵抗 Ｒ を流れる電流は，

ｉ ＝ e1 / R1 (7)

である。 演算増幅器の入力インピーダンスは無限大のため， この電流は全てコンデンサ Ｃ を流れる。 これより，コンデンサ Ｃ に発生する電圧は，

[コンデンサ Ｃ に発生する電圧の大きさ] ＝ Ｑ ／ Ｃ ＝ (１／Ｃ) ∫ｉ dt (8)

である。 ただし，Ｑはコンデンサに蓄積された電荷量である。 電流の方向，反転入力端子の電位を考慮に入るならば， 出力電圧 ｖout は，

ｖout ＝ − (１／ＣＲ) ∫ e1 dt (9)

となる。


実行例

回路を組むときの注意
課題

(5) 非反転増幅器（正相増幅器）

前述の二つの増幅器では，入力電圧と出力電圧は符号が逆であったが， 等しい符号の出力を取りだせる回路もある．それが図５に示す非反転増幅回路 （正相増幅回路）である． この回路でも，負帰還の働きで仮想ショートが成立ち，反転入力端子の電位は， 正相入力端子の電位と等しいため，ｖ２ ＝ ｖ１ となる． また，演算増幅器の入力インピーダンスが無限大のため， 抵抗 Ｒ と Ｒ' には同じ大きさの電流が流れる．そのため， 入力電圧 ｖｉｎ と 出力電圧 ｖｏｕｔ の関係は，

ｖout ＝ Ｒ ＋ Ｒ'
Ｒ 		ｖｉｎ ＝ （１＋ Ｒ'
Ｒ		 ）ｖｉｎ
(10)

で与えられる。


実行例

回路を組むときの注意
課題

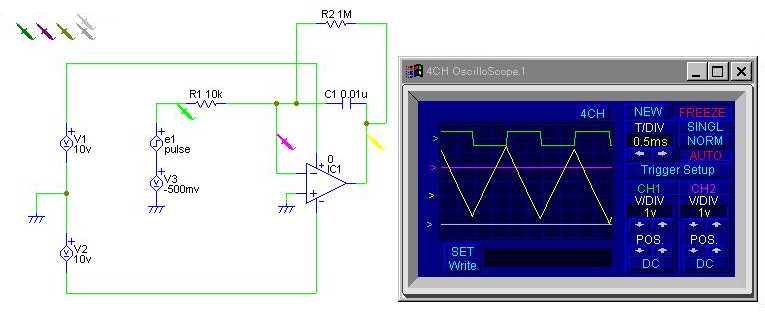
(6) 発振器


実行例

回路を組むときの注意
課題

その他，自由に回路を作ってみよう

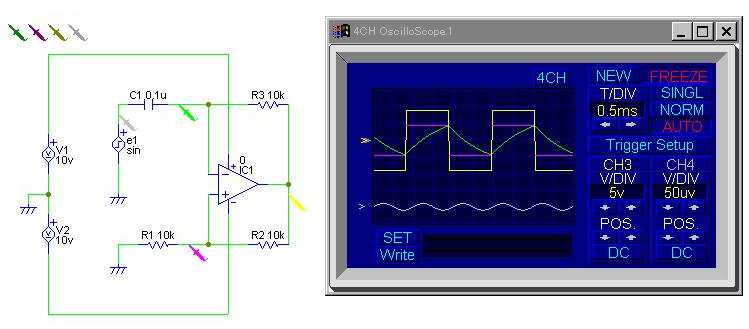
例1:差動増幅器

二つの入力信号 e1 と e2 の差を増幅する差動増幅回路を次に示す。 この回路は， ちょうど反転増幅回路と非反転増幅回路を組み合わせている。 出力電圧は，

ｖout ＝ (Ｒ'/Ｒ) e2 − (Ｒ'/Ｒ) e1 (11)

で与えられる。ただし，R2 ＝ R4 ＝ R'， R1 ＝ R3 ＝ R とする。


実行例↑

回路を組んだ時の注意

例2:？？？回路

トランジスタ Q1 の上にある，緑の四角形は， 負荷抵抗を表わす。
もしも，この回路図を参考に回路動作をチェックしたければ， 四角形の代わりに，抵抗や，コンデンサなどを入れてみれば良い。
ヒント:
"何を入れてもよい"ということは，「どんな時でも同じ動作をする」 と考えられる。 回路動作から考えると，どんな時でも同じ動作をするものとして直ぐに思い浮かぶのは， "電源"である。 電源には定電圧源と定電流源の2種類あるが， いずれの場合にも回りの回路によらず一定の電圧(または電流)を供給する。


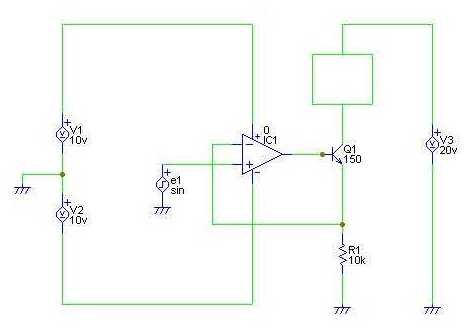
注：この回路はこのままでは動きません。↑

V. 考察課題

(1)各実験それぞれの課題について考察せよ。
(2)差動増幅器の出力の式(11)を説明せよ。
(3)例2 の回路の回路動作を説明せよ。

VI. 参考文献

アナログ電子回路（藤井信生）昭晃堂 1984年

　

以上.