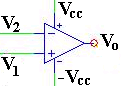
図1 op-ampの回路図
2003 2/24 加算回路回り小変更
2002 1/30 加算回路回り小変更
'01 2/13 変更
'98 11/19 小変更
'98 10/15 by 望月
|
☆ここで,回路を習得するとあるが,望月は"習得"について次のように考えています。 「習得したとは,回路図を見ただけで,回路の真の動作がわかるということである。 習得した学生には,作った回路の特性を測定したり, シミュレーションして出てきた結果は,予想通りのものとなる。」 従って, |
演算増幅器は, もともとアナログ電子計算機に用いられていた高利得の増幅器で, 加減算,微積分,その他の演算に用いられていた。 集積回路技術の進歩と共に,演算増幅器も集積回路され, 一般の回路に用いられるようになった。 演算増幅器を用いることにより, 増幅回路を始め種々の演算回路を容易にしかも高性能に実現することが出来る。 時には個別部品(トランジスタやダイオード単体) を組み合わせて回路を設計するよりも, 簡単でかつ特性の優れた回路が得られる。
本実験では,演算増幅器の原理,基本的な使い方, 及びいくつかの応用回路を習得する。
演算増幅器(Operational Amplifier, op-amp)は, 図1に示すように3つの端子で出来た素子であり, −(マイナス)で示される反転入力端子と, +(プラス)で示される正相入力端子(または非反転入力端子) の二つの入力端子に加えられた電位差を増幅し, 出力端子に出力する働きをする。
それぞれの入力端子に,電圧 V1 , V2 を加えると,出力電圧 Vo は
| Vo = Ad * (V1 − V2) | (1) |
となる。この時, Ad を差動利得という。
どちらの入力端子に, 電圧 Vin を加えたときの入力電流 Iin の関係は, 入力インピーダンス Zin で表わされる。
| (2) |
なお,演算増幅器は一つの電子回路であるから, 上記の特性を実現するには電源が不可欠である。 図1では Vcc と -Vcc が電源の配線である。 この配線は余りにも当然過ぎるため回路図で省略されることが多いが,極めて重要である。 稚拙な電源配線をした場合には電気的特性が低下する可能性が高いので,注意したい。

演算増幅器として要求される理想的な特性と, 実際の演算増幅器の特性の比較を表1に示す。 表からわかるように,実際の演算増幅器はほとんど理想に近い特性である。 そのため,演算増幅回路を含む回路を解析する時には, 理想特性を示す素子と仮定してもよい。
| パラメータ | 理想特性 | μA741 | LF356 |
|---|---|---|---|
| 差動利得 Ad | ∞ | 100 [dB] 以上 | 100 [dB] 以上 |
| 入力インピーダンス | ∞ | 2 [MΩ] | 106 [MΩ] |
| 出力インピーダンス | 0 | 50 [Ω] | 50 [Ω] |
| 帯域幅(−3 [dB]) | ∞ | 10 [Hz] | 10 [Hz] |
演算増幅器には,大きく分けて二つの使い方がある。 一つは比較器でもう一つは増幅器である。
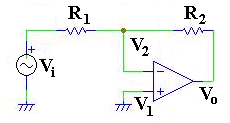
図1の回路は,比較器(コンパレータ)として動作する。 比較器は,入力 V1, V2 それぞれに別々の入力電圧を加え, 1つの出力電圧を取り出すものである。 このとき,出力電圧は式(1)で与えられ,正か負の非常に大きな電圧が現れることが予想される。 ところが演算増幅器の出力電圧は電源電圧範囲内に制限されるため, 実際には,+Vcc または -Vcc 以内の電圧しか出力できない。 従って,出力電圧には,二つの入力電圧のどちらの電圧が高いか, という情報しか出力されないことになる。 数学的に考えると,V1 = V2 の時には Vo = 0 になるはずであるが, Ad が極めて大きいことを考えると, 工学的にはそういう状態は殆んど考慮する必要がない。 入力条件と出力電圧の関係を表2に示す。 比較器は,アナログ信号をデジタル信号に変換する回路, または,デジタル信号伝送回路の受信部で用いられる.
| 入力条件 | 理想出力電圧 | 実際の出力電圧 (注意) |
|---|---|---|
| V1 > V2 | +∞ [V] | +15 [V] |
| V1 < V2 | −∞ [V] | −15 [V] |
| 例えば,V1 =1[V],V2 =2[V] | −∞ [V] | −15 [V] |
図2の回路を,反転増幅器と呼ぶ。 この回路では,入力信号が増幅され,出力端子から出力される。 もしも正弦波の入力であれば,出力信号も正弦波である。 出力電圧は,基本的には電源電圧よりも小さな電圧となり, ±Vcc に飽和することはない。 出力端子電圧の絶対値が電源電圧よりも小さいということは, V2 =
仮想ショートが成り立つ理由は,出力端子の電圧がマイナス入力の端子に接続されたことによる。 この配線方法は「負帰還」と名づけられている。 表3に,図2の回路にノイズが入った場合の回路動作を示す。 ノイズが入った時,回路内でつじつまを合わせ, 差動入力端子と同相入力端子の電位差がゼロになることがわかる。
負帰還を含む増幅回路の特性を解析するときには, 入力電圧と,V2 =
| 回路の状態 | 入力電圧 | 出力電圧 | 正相入力端子の電圧 V1 | 反転入力の電圧 V2 |
|---|---|---|---|---|
| 初期状態 | Vi(固定) | Vo | V1は常に0[V] | V2 = V1 (=0[V]) |
| 仮定 | Voにノイズが入り, Vo の電圧上昇 | |||
| 経過1 | Vo の上昇に伴い, V2は上昇 | |||
| 経過2 | V2 の電圧上昇に伴い, Vo は電圧下降 | |||
| 結果 | Vo はもとの電圧に戻る。 | V2 は元の電圧に戻る。 |
op-ampを使った回路を説明すると共に, 実験手順と,実験の課題を述べる。
実行例
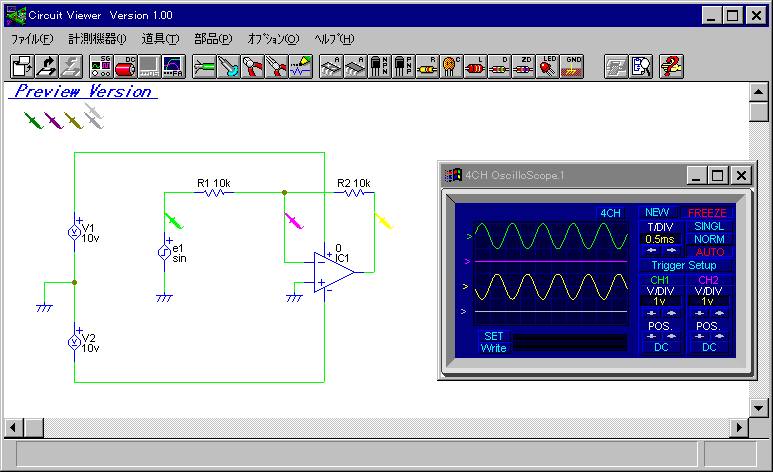
次に示すのは負帰還増幅回路である。
演算増幅器と抵抗 R1 と R2 によって構成されている。
この回路の電圧増幅率を計算しよう。
負帰還がかかっているため,常に仮想ショートが成り立つため,
反転入力端子の電位は,非反転入力端子の電位と同じく 0V になる。
入力電圧 e1 を与えた時,
この時,抵抗 R1 を流れる電流は,
| iR1 = (e1 - 0[V]) / R1 = e1 / R1 | (3) |
である。 演算増幅器の入力インピーダンスは ∞ [Ω] のため, この電流は全て抵抗 R2 を流れる。 これより,抵抗 R2 の両端に発生する電位差は,
| [抵抗 R2 に発生する電圧] = iR2 * R2 = iR1 * R2 | (4) |
である。 反転入力端子の電位が 0 [V] であることと, 電流の流れの方向を考慮に入れ, 入力電圧 e1 と 出力電圧 vout の関係を求めるならば,式(5)が求められる。
| vout = − (R2/R1) * e1 . | (5) |
実行例
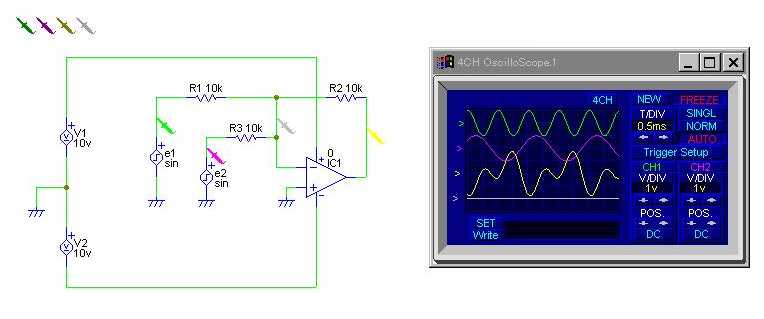
加算器の回路を次に示す。 この回路は,反転増幅器の回路を拡張したものである。 この回路でも,演算増幅器の入力インピーダンスは無限大であり, 2つの入力端子には仮想ショートが成立つことから, 出力電圧は,
| vout = − (R2 / R1) * e1− (R2 / R3) * e2 | (6) |
で与えられる。 もしも,入力部の2つの抵抗値が等しく,いずれも R ならば,出力電圧は,
| vout = − (R2 / R) *(e1 + e2) | (7) |
となる.
この回路では2入力の加算器を示したが,
容易に3入力以上の加算器に応用できる。
実行例
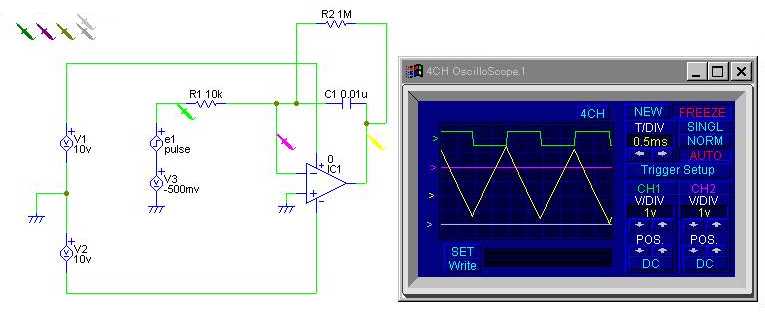
能動素子を使用しないで抵抗とコンデンサだけで積分回路を構成すると,
回路は図7のようになる。
この回路では,信号の周期が回路の時定数 τ = RC
よりも充分に小さくなければ出力信号に誤差が生じてしまう。
図8に破線で,
この回路にステップファンクション信号が入った時の出力信号を示す。
図8に実線で,演算増幅器を使った積分器の出力信号を示す。
このとき,回路は図9である。
この回路でも負帰還の働きで仮想ショートが成立つため,
反転入力端子の電位は 0[V] である。
この時,抵抗 R を流れる電流は,
| i = e1 / R1 | (8) |
である。 演算増幅器の入力インピーダンスは無限大のため, この電流は全てコンデンサ C を流れる。 これより,コンデンサ C に発生する電圧は,
| [コンデンサ C に発生する電圧の大きさ] = Q / C = (1/C) ∫i dt | (9) |
である。 ただし,Qはコンデンサに蓄積された電荷量である。 電流の方向,反転入力端子の電位を考慮に入るならば, 出力電圧 vout は,
| vout = − (1/CR) ∫ e1 dt | (10) |
となる。
実行例
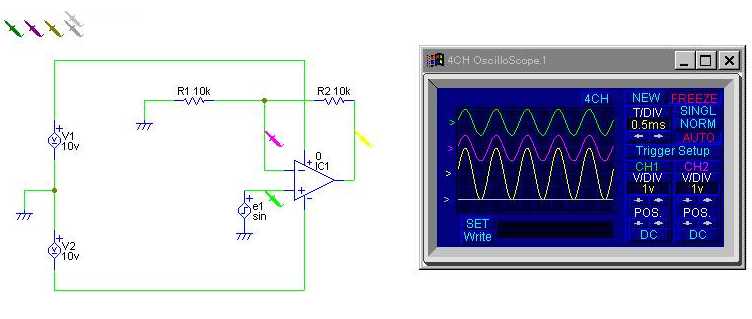
前述の二つの増幅器では,入力電圧と出力電圧は符号が逆であったが, 等しい符号の出力を取りだせる回路もある.それが図5に示す非反転増幅回路 (正相増幅回路)である. この回路でも,負帰還の働きで仮想ショートが成立ち,反転入力端子の電位は, 正相入力端子の電位と等しいため,V2 = V1 となる. また,演算増幅器の入力インピーダンスが無限大のため, 抵抗 R と R' には同じ大きさの電流が流れる.そのため, 入力電圧 vin と 出力電圧 vout の関係は,
| (11) |
で与えられる。
実行例

実行例
二つの入力信号 e1 と e2 の差を増幅する差動増幅回路を次に示す。 この回路は, ちょうど反転増幅回路と非反転増幅回路を組み合わせている。 出力電圧は,
| vout = (R'/R) e2 − (R'/R) e1 | (12) |
で与えられる。ただし,R2 = R4 = R', R1 = R3 = R とする。

実行例↑
トランジスタ Q1 の上にある,緑の四角形は,
負荷抵抗を表わす。
もしも,この回路図を参考に回路動作をチェックしたければ,
四角形の代わりに,抵抗や,コンデンサなどを入れてみれば良い。
ヒント:
"何を入れてもよい"ということは,「どんな時でも同じ動作をする」
と考えられる。
回路動作から考えると,どんな時でも同じ動作をするものとして直ぐに思い浮かぶのは,
"電源"である。
電源には定電圧源と定電流源の2種類あるが,
いずれの場合にも回りの回路によらず一定の電圧(または電流)を供給する。
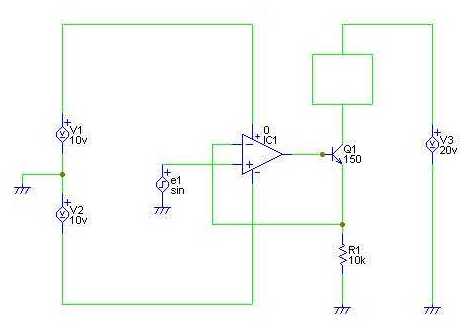
注:この回路はこのままでは動きません。↑
茶 赤 橙 = 1 2 3 = 22. × 103 = 12. kΩ |
|
抵抗値の読み方と同様のルールが適用されるが,次の2点が抵抗の場合と異なる。 ・数値がそのまま印刷されているので,色などと数値との対応を新たに覚える必要がない ・単位の基本は pF (ピコ ファラッド = 10-12 ファラッド)である 例: 2 2 4 = 22. × 104 pF = 220. nF = 0.22 μF なお,マイクロファラッドのオーダの容量では,そのまま値を印刷してあるものもあります。 |
IC(Integrated Circuit = 集積回路) は,黒いプラスチックパッケージに,2列になってたくさんの端子がついた形が基本的な形である。
IC がどういう機能を持っているか,どのように調べたらよいか,以下にまとめる。
|
|
オシロスコープ上で観測した波形が,正弦波や三角波などよく知られた波形だった場合には,
その振幅を測定する際に,最大値と最小値の差を測り,
その値を Vpp (ピークtoピーク電圧)で記録します。 例えば,100[V]の商用電源の場合,
ピークtoピークを測定を,最大値の測定を比べると, いちいちGNDレベルを設定しなおす必要が無いため素早い測定が可能であり, レンジが倍になるため精度も上がるというメリットがあります。 しかし,この測定方法を当てはめることの出来る波形は, 単一の電圧情報で表わすことの出来るものに限られますので,注意しましょう。 |
回路シミュレータの起動実験の準備のために以下の処理をして下さい。
ソフトの使用法についてソフトは直感的に使えると思います。以下に,質問の多かったことについて,まとめます。
|
☆レポートの効率的な書き方の例をこっそり(!?)教えます。
|
|
☆画像のワープロへの取込み Windows上のソフトウエアで画面上に描かれた画像は, 次の操作でワープロ上に貼り付けることが可能です。
|
以上.