1.制御電源を使った非線形特性の表現の確認
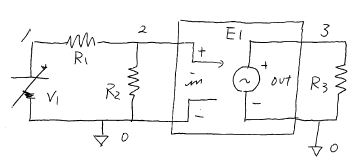ファイル ' ne141.cir ' の中身。 Download* circuit e141 * Check NonLinear .DC V1 -2.2 2.2 0.02 V1 1 0 6 R1 1 2 1k R2 0 2 1k R3 3 0 1k E1 3 0 poly(1) (2,0) 0 0 0 1 .probe .END
※ne141は，na101を下地に作ったファイルです。 回路 ne141 は，ngspice において「非線形特性が実現できる」ことを体験する教材である。 回路 ne141 をシミュレーションするための操作 (1) ngspice の起動 (2) 「file」＞「open」から ne141.cir を開く (3) 「file」＞「run」 コマンドによるシミュレーションの実行 (4) 「Graph」＞「Select Vector」コマンドを選ぶ --->すると，表示すべき電圧を聞いてくる。 (5) v(1) v(2) v(3) と打ち込む (6) (お好みで)「Command」＞「Edit source」から編集すればパラメタを変えられる。 DC解析は，直流電圧を変えたときの出力を見ることである。 ここで，R2 に加わる電圧を，E1 という「電圧制御電圧源」によって，R3 に加わる電圧に変換する。 その際に，POLY オプションを使うことによって，非線形性を実現している。 ---課題： E1 3 0 poly(1) (2,0) 0 0 0 1 ← これは(2,0)の端子間電圧を３乗して3,0 の端子間電圧にする。 E1 3 0 poly(1) (2,0) 0 0 1 0 ← これは２乗特性。 E1 3 0 poly(1) (2,0) 0 5 0 0 ← これは比例特性。 E1 3 0 poly(1) (2,0) 5 0 0 0 ← これは０乗特性（＝定数） 注意：課題の３行目（比例）は，次の３行のいずれとも同じである。 E1 3 0 poly(1) (2,0) 0 5 0 E1 3 0 poly(1) (2,0) 0 5 E1 3 0 2 0 5 注意：4行目（定数）は，次の行と同一である。 注意：課題の４行目（比例）は，次の４行のいずれとも同じである。 E1 3 0 poly(1) (2,0) 5 0 0 E1 3 0 poly(1) (2,0) 5 0 E1 3 0 poly(1) (2,0) 5 V1 3 0 DC 5
2.制御電源による単純な抵抗や非線形特性を持つ抵抗の実現
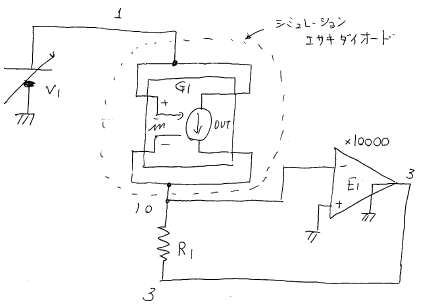ファイル ' ne142.cir ' の中身。 Download
* circuit e142 * make Esaki Diode Simulator .DC V1 -0.1 0.6 0.02 V1 1 0 6 E1 3 0 0 10 10000 R1 10 3 1k G1 1 10 poly(1) (1,10) 0 0.063 -0.27 0.3 *G1 1 10 poly(1) (1,10) 0 0.063 .probe .END
※ne142は，na102を下地に作ったファイルです。 回路 ne142 は，G を用いることで非線形の特性を代替できることを確認する教材である。 なお，G とは電圧制御電流源をシミュレーションする素子のことである。 ここでは江崎ダイオードを想定した。このダイオードの電圧電流特性の例を次に上げる。 回路 ne142 内の G1 という素子が，この電圧電流特性を実現している。この回路は，素子E1（電圧制御電圧源）が，ちょうど演算増幅器として働き， ノード「10」が仮想接地点となり，素子 G1 と抵抗 R1 には同じ電流が流れる。 したがって，R1の両端に現われる電圧を見ると，G1 に流れる電流値が推察できる。 回路 ne142 をシミュレーションするための操作 (1) ngspice の起動 (2) 「file」＞「open」から ne142.cir を開く (3) 「file」＞「run」 コマンドによるシミュレーションの実行 (4) 「Graph」＞「Select Vector」コマンドを選ぶ --->すると，表示すべき電圧を聞いてくる。 (5) v(1)-v(10) v(10)-v(3) と打ち込む (6) (お好みで)「Command」＞「Edit source」から編集すればパラメタを変えられる。 注意：v(1)-v(10) とは，素子 G1 に加わる電圧 注意：v(10)-v(3) とは，抵抗 R1 に加わる電圧であるが，この値は，R1 に流れる電流に比例し， その電流はそのまま素子 G1 に流れる。従って，v(10)-v(3) は素子 G1 に流れる電流とみて良い。 もしも，G1という素子を，現在コメントアウトしているものと置き換えると，単純な抵抗として働く。
(3. skip)
4."ミラー効果"の利用により単体のコンデンサとは異なる容量を実現する
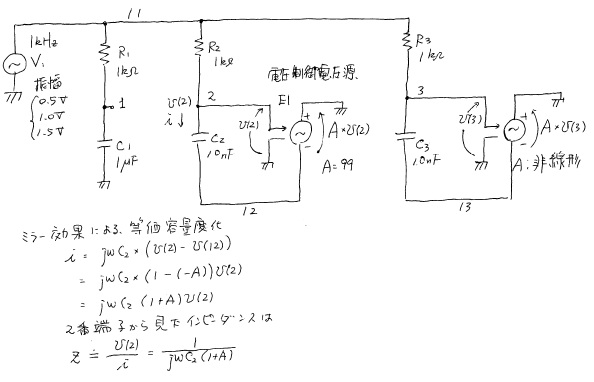ファイル ' ne144.cir ' の中身。 Download* circuit e144 * Check NonLinear Capacitor .tran 100n 6m 0 V1 11 0 sin(0 1.0V 500) R1 11 1 1k C1 1 0 1uF R2 11 2 1k C2 2 12 10nF E2 0 12 2 0 100 R3 11 3 1k C3 3 13 10nF E3 0 13 poly(1) (3,0) 0 89 0 90 .probe .END
※ne144は，na106を下地に作ったファイルです。
これは spice にて「コンデンサ等でも非線形特性が実現できる」ことを理解する教材である。 回路 ne144 をシミュレーションするための操作 (1) ngspice の起動 (2) 「file」＞「open」から ne144.cir を開く (3) 「file」＞「run」 コマンドによるシミュレーションの実行 (4) 「Graph」＞「Select Vector」コマンドを選ぶ --->すると，表示すべき電圧を聞いてくる。 (5) v(1) v(2) v(3) と打ち込む (6) (お好みで)「Command」＞「Edit source」から編集すればパラメタを変えられる。 （課題）V1 の振幅を，0.3[V], 1.0[V]，3.0[V] と変更したときの応答を見てみよう。 この回路は，ひとつの電源V1と， R1とC1からなる分路1と， R2とC2と制御電源E2からなる分路2と， R3とC3と制御電源E3からなる分路3 から出来ている。 抵抗は，R1=R2=R3=1kΩである。 容量は，V1の振幅が1[V]のときに，どれも1μF として働くように，定数を調整してある。 分路1は，まさに文字通りのRC回路であり，特に解説は不要であろう。 分路2は，使われている容量は10nFであるが，制御電源をつかった「ミラー効果」によって 等価的な容量値を100倍（＝ 1+A 倍）にしている。 今回の課題では，どの条件のときも，分路1と同じ結果が得られるはずである。 分路3は，ミラー効果を利用して等価的な容量値を増やしているが，制御電源に非線形性を 含めたために，等価的な容量も非線形性を持っている。 従って， ・V1の振幅が0.3[V]のときは，等価的な容量値がC1よりも小さいため，V(3)はV(1)より大きい， ・V1の振幅が1.0[V]のときは，等価的な容量値がC1とほぼ同じになるため，V(3)はV(1)とほぼ同じ， ・V1の振幅が3.0[V]のときは，等価的な容量値がC1よりも大きいため，V(3)はV(1)より小さい， という結果が得られる。
5. コンデンサのどちらもグランドに接続していなくても非線形を実現
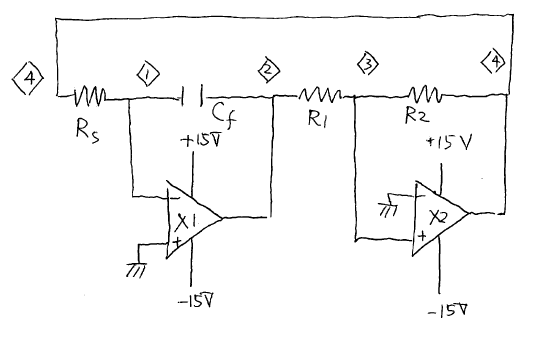図145(a)ファイル ' ne145.cir ' の中身。 Download
* circuit e145 * Check NonLinear Capacitor .tran 100n 3.0m 0 Rs 4 1 2k *Rf 1 2 2M X1 0 1 2 opamp00 X2 3 0 4 opamp00 R1 3 2 1k R2 3 4 15k Cf 1 10 1u Vf 10 2 dc 0 ac 0 Fx 20 0 Vf 1 Rx 20 0 1k Bf 1 2 I=0 *Bf 1 2 I= I(Vf)*V(1,2)*V(1,2)/10 ; Cf' ... nonlinear *Bf 1 2 I= 1.0 * I(Vf) ; Cf' = 2.0 * Cf *Bf 1 2 I= 0.5 * I(Vf) ; Cf' = (3/2)* Cf *Bf 1 2 I= 0.0 * I(Vf) ; Cf' = 1.0 * Cf *Bf 1 2 I= -0.5 * I(Vf) ; Cf' = 0.5 * Cf *Bf 1 2 I= -0.75 * I(Vf) ; Cf' = (1/4)* Cf .probe *------------------------------------------------ * copy form * http://www.madlabo.com/mad/edat/spice/index.htm *------------------------------------------------ * HItachi Si EP High speed switch .model d1s2075 D(IS=1.387E-9 N=1.702 RS=1.53 + CJO=1.92pf VJ=0.4996 M=0.0605 TT=5ns BV=75 IBV=100E-15) * *Low Noise Amp PC=0.4W Ic=0.15A Vcbo=60V .model Q2SC1815 NPN(Is=2.04f Xti=3 Eg=1.11 Vaf=6 Bf=400 Ne=1.5 + Ise=0 Ikf=20m Xtb=1.5 Br=3.377 Nc=2 Isc=0 Ikr=0 Rc=1 Cjc=2p + Mjc=.3333 + Vjc=.75 Fc=.5 Cje=5p Mje=.3333 Vje=.75 Tr=10n Tf=311.1p + Itf=0 Vtf=0 Xtf=0) * TOSHIBA 90-01-29 creation * *Low Noise Amp PC=0.4W Ic=0.15A Vcbo=50V .model Q2SA1015 PNP(Is=295.1E-18 Xti=3 Eg=1.11 Vaf=100 Bf=110 Ne=1.5 + Ise=0 Ikf=0 Xtb=1.5 Br=10.45 Nc=2 Isc=0 Ikr=0 Rc=15 Cjc=66.2p + Mjc=1.054 Vjc=.75 Fc=.5 Cje=5p Mje=.3333 Vje=.75 Tr=10n + Tf=1.661n Itf=0 Vtf=0 Xtf=0) * TOSHIBA 90-01-23 creation * * Ideal Operational Amplifier . . . K. Mochizuki 2002.3.15 * + - out .subckt opamp00 50 51 55 rin 50 51 1G cin 50 51 5p e1st 52 0 50 51 100000 r53 0 52 1g r51 52 53 100k c51 0 53 53n d51 56 53 d1s2075 d52 53 57 d1s2075 v51 56 0 -13.7V v52 57 0 13.7V r52 53 54 1k c52 0 54 53p d53 58 54 d1s2075 d54 54 59 d1s2075 v53 58 0 -13V v54 59 0 13V eout 55 0 54 0 1 rpow 55 0 1G .ends *----------------------------------------------------- .END
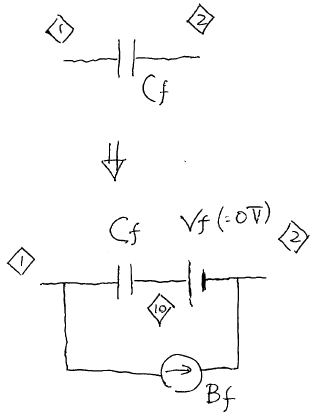図145(b)
※ne145は，オリジナルファイルです。 これは spice にてコンデンサのどちらもグランドに接続していなくても非線形を実現することを理解する教材です。 回路 ne145 をシミュレーションするための操作 (1) ngspice の起動 (2) 「file」＞「open」から ne145.cir を開く (3) 「file」＞「run」 コマンドによるシミュレーションの実行 (4) 「Graph」＞「Select Vector」コマンドを選ぶ --->すると，表示すべき電圧を聞いてくる。 (5) v(2) v(20) v(3) v(4) と打ち込む。（なお，ここで指定した v(20) は，Cf に流れる電流を観測するためのものである） (6) (お好みで)「Command」＞「Edit source」から編集すればパラメタを変えられる。 注意1：この回路は，積分回路を利用した弛張発振回路である。 この回路の動作は，容量 Cf の両端の電位差が決められた値に達するごとに回路の極性が変化し， 発振が続くというものである。 このことから， ・容量 Cf が大きくなると， 注意2：この回路では，容量「Cf」について，Vf と Bf の働きによって，非線形性を導入できる。 注意3：この回路の Fx と Rx は，Cf に流れる電流をグラフ化するためのものであり，無くても動作に影響しない。 （基準）上記の回路そのままの状態でシミュレーションしてみよう。これを基準にします。 （準備1）基準の回路において，容量 Cf を 2u （2μF）に変更してシミュレーションしてみよう。 これにより，（基準）の場合と比べて積分の時間が 2 倍になり，1周期の長さも2倍になる。 この操作（準備1）が終わったら，容量 Cf を 1u （1μF） に戻そう。 （準備2）基準の回路において，抵抗 R1 を 2kΩ に変更してシミュレーションしてみよう。 これにより，（基準）の場合と比べて V(2)の振幅が2倍になり，1周期の長さも2倍になる。 この操作（準備1）が終わったら，抵抗 R1 を 1kΩ に戻そう。 （容量の増減）ファイル内の， 「Bf 1 2 I= 0」という行を，次のそれぞれの行にならって書き換えてみよう。 *Bf 1 2 I= 1.0 * I(Vf) ; Cf' = 2.0 * Cf *Bf 1 2 I= 0.5 * I(Vf) ; Cf' = (3/2)* Cf *Bf 1 2 I= 0.0 * I(Vf) ; Cf' = 1.0 * Cf *Bf 1 2 I= -0.5 * I(Vf) ; Cf' = 0.5 * Cf *Bf 1 2 I= -0.75 * I(Vf) ; Cf' = (1/4)* Cf この操作をすると，あたかも容量値が増加（または減少）したかのように振舞うことを確認しよう。 なお，B という素子は，数式を書ける電源である。今回は電流源として使用している。 こうした大きさの電流が流れることで，どうして容量が増減するのか考察してみよう。 （非線形な容量）ファイル内の， 「Bf 1 2 I= 0」 という行を，次の行のように書き換えてシミュレーションをしよう。 「Bf 1 2 I= I(Vf)*V(1,2)*V(1,2)/10 」 続いて，抵抗 R1 を 2kΩ に変更してシミュレーションしてみよう。 容量が線形だった時は，周期の長さは R1 の大きさに比例していた。 しかし，今回は非線形性を導入しており，周期の長さは R1 の大きさに比例しているわけではない。
6. コイルについて，5.のコンデンサと同様に非線形を実現
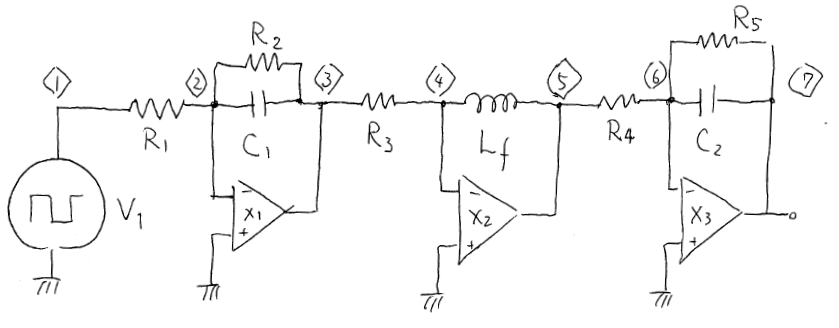図146(a)ファイル ' ne146.cir ' の中身。 Download準備中
* circuit e146 * Check NonLinear Liactance .tran 100n 1.5m 0 .ic V(2)=0, V(3)=0 Vin 1 0 pulse(1V -1V 0.1ms 0 0 0.2ms 0.4ms) X1 0 2 3 opamp00 X2 0 4 5 opamp00 X3 0 6 7 opamp00 R1 1 2 1k C1 2 3 0.1u R2 2 3 1MEG R3 3 4 1k R4 5 6 100 C2 6 7 1u R5 6 7 1MEG *Lf 4 5 0.01m Vf 9 5 dc 0 ac 0 Lf 8 9 0.01m *BVL 4 8 V= V(8,9) *BVL 4 8 V= 1.0 * V(8,9) ; Lf' = 2.0 Lf *BVL 4 8 V= 0.5 * V(8,9) ; Lf' = 1.5 Lf BVL 4 8 V= 0.0 * V(8,9) ; Lf' = 1.0 Lf *BVL 4 8 V=-0.5 * V(8,9) ; Lf' = 0.5 Lf *BVL 4 8 V=-0.75* V(8,9) ; Lf' = 0.25Lf *BVL 4 8 V= 10 * V(8,9) /(1 + 10000000000000000*(I(Vf))^4 ) ; Lf' ... nonlinear *BVL 4 8 V= 10 * V(8,9) /(1 + 10000000000000000*(I(Vf)- 0.0001 * V(8,9)/abs(V(8,9)) )^4 ) .probe *------------------------------------------------ * copy form * http://www.madlabo.com/mad/edat/spice/index.htm *------------------------------------------------ * HItachi Si EP High speed switch .model d1s2075 D(IS=1.387E-9 N=1.702 RS=1.53 + CJO=1.92pf VJ=0.4996 M=0.0605 TT=5ns BV=75 IBV=100E-15) * *Low Noise Amp PC=0.4W Ic=0.15A Vcbo=60V .model Q2SC1815 NPN(Is=2.04f Xti=3 Eg=1.11 Vaf=6 Bf=400 Ne=1.5 + Ise=0 Ikf=20m Xtb=1.5 Br=3.377 Nc=2 Isc=0 Ikr=0 Rc=1 Cjc=2p + Mjc=.3333 + Vjc=.75 Fc=.5 Cje=5p Mje=.3333 Vje=.75 Tr=10n Tf=311.1p + Itf=0 Vtf=0 Xtf=0) * TOSHIBA 90-01-29 creation * *Low Noise Amp PC=0.4W Ic=0.15A Vcbo=50V .model Q2SA1015 PNP(Is=295.1E-18 Xti=3 Eg=1.11 Vaf=100 Bf=110 Ne=1.5 + Ise=0 Ikf=0 Xtb=1.5 Br=10.45 Nc=2 Isc=0 Ikr=0 Rc=15 Cjc=66.2p + Mjc=1.054 Vjc=.75 Fc=.5 Cje=5p Mje=.3333 Vje=.75 Tr=10n + Tf=1.661n Itf=0 Vtf=0 Xtf=0) * TOSHIBA 90-01-23 creation * * Ideal Operational Amplifier . . . K. Mochizuki 2002.3.15 * + - out .subckt opamp00 50 51 55 rin 50 51 1G cin 50 51 5p e1st 52 0 50 51 100000 r53 0 52 1g r51 52 53 100k c51 0 53 53n d51 56 53 d1s2075 d52 53 57 d1s2075 v51 56 0 -13.7V v52 57 0 13.7V r52 53 54 1k c52 0 54 53p d53 58 54 d1s2075 d54 54 59 d1s2075 v53 58 0 -13V v54 59 0 13V eout 55 0 54 0 1 rpow 55 0 1G .ends *----------------------------------------------------- .END
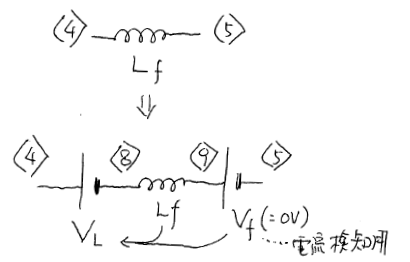図146(b)
※ne146は，オリジナルファイルです。 これは spice にてコンデンサのどちらもグランドに接続していなくても非線形を実現することを理解する教材です。 回路 ne146 をシミュレーションするための操作 (1) ngspice の起動 (2) 「file」＞「open」から ne146.cir を開く (3) 「file」＞「run」 コマンドによるシミュレーションの実行 (4) 「Graph」＞「Select Vector」コマンドを選ぶ --->すると，表示すべき電圧を聞いてくる。 (5) v(1) v(3) v(5)*9900 v(7)*9900 と打ち込む。 ---> １万倍に拡大して波形観察したいため，V(5)とV(7)に対して *9900 とした。 ---> V(1) などとぴったり重なるのを避けるため，ぴったりの 10000 ではなく 9900 にした。 (6) (お好みで)「Command」＞「Edit source」から編集すればパラメタを変えられる。 注意1：この回路の各部の波形は，<1>と<5>は方形波，<3>と<5>は三角波である 注意2：この回路において，次の(赤い字のように)修正をして走らせると，リアクタンスは倍になる。 *Lf 4 5 0.01m Vf 9 5 dc 0 ac 0 Lf 8 9 0.01m *BVL 4 8 V= V(8,9) BVL 4 8 V= 1.0 * V(8,9) ; Lf' = 2.0 Lf *BVL 4 8 V= 0.5 * V(8,9) ; Lf' = 1.5 Lf *BVL 4 8 V= 0.0 * V(8,9) ; Lf' = 1.0 Lf *BVL 4 8 V=-0.5 * V(8,9) ; Lf' = 0.5 Lf *BVL 4 8 V=-0.75* V(8,9) ; Lf' = 0.25Lf *BVL 4 8 V= 10 * V(8,9) /(1 + 10000000000000000*(I(Vf))^4 ) ; Lf' ... nonlinear *BVL 4 8 V= 10 * V(8,9) /(1 + 10000000000000000*(I(Vf)- 0.0001 * V(8,9)/abs(V(8,9)) )^4 ) 注意3：この回路では，誘導「Lf」について，Vf と BVL の働きによって，非線形性を導入できる。 （基準）上記の回路そのままの状態でシミュレーションしてみよう。これを基準にします。 （準備1）基準の回路において，リアクタンス Lf を 0.02mH に変更してシミュレーションしてみよう。 これにより，電圧 V(5) の振幅が（基準）の場合と比べて2倍になり，電圧 V(7) の振幅も2倍になる。 この操作（準備1）が終わったら，リアクタンス Lf を 0.01mH に戻そう。 （リアクタンスの増減）ファイル内の， 「BVL 4 8 V= V(8,9)」という行を，次のそれぞれの行にならって書き換えてみよう。 *BVL 4 8 V= 1.0 * V(8,9) ; Lf' = 2.0 Lf *BVL 4 8 V= 0.5 * V(8,9) ; Lf' = 1.5 Lf *BVL 4 8 V= 0.0 * V(8,9) ; Lf' = 1.0 Lf *BVL 4 8 V=-0.5 * V(8,9) ; Lf' = 0.5 Lf *BVL 4 8 V=-0.75* V(8,9) ; Lf' = 0.25Lf この操作をすると，あたかも容量値が増加（または減少）したかのように振舞うことを確認しよう。 なお，B という素子は，数式を書ける電源である。今回は電圧源として使用している。 こうした大きさの電圧が加わることで，どうしてリアクタンスが増減するのか考察してみよう。 （非線形な容量）ファイル内の「BVL」の部分を，次の行に置き換えてみよう。 BVL 4 8 V= 10 * V(8,9) /(1 + 10000000000000000*(I(Vf))^4 ) ; Lf' ... nonlinear これによって，電流が小さいときだけに，コイルに大きな電圧が発生するようになる。 これは，ちょうど軟質磁性材料（ヒステリシスが小さくなるよう純度を上げた鉄）の磁気特性に似せたものである。 こうした材料は，コイルの芯材料として用いられる。 また，ファイル内の「BVL」の部分を，次の行に置き換えてみよう。 *BVL 4 8 V= 10 * V(8,9) /(1 + 10000000000000000*(I(Vf)- 0.0001 * V(8,9)/abs(V(8,9)) )^4 ) これによって，電流が増えるときと減るときでは，電圧が発生する電流値が変わっている。 これは，ちょうど硬質磁性材料（ヒステリシスが大きくなるように不純物や欠陥を導入した鉄）の磁気特性に似せたものである。 こうした材料は，永久磁石の材料として用いられる。