先の題材(振り子の運動)を元に,
外力が加わった場合と,パラメトリック振動を取り扱う。
物理的な意味を考えるため,方程式は敢えて物理的なものに遡る。
なお,方程式は次のものに書き換る。
m L x'' = - a L x' - g sin(x) + F(t)
変数 x [rad] は振り子の角度,
パラメタ L [m] は振り子の棒の長さ,
記号 ' は時間による微分,
パラメタ m [kg] は質量,
パラメタ a [kg/s] は空気抵抗,
パラメタ g [kg m/s2] は重力加速度,
関数 F(t) [kg m/s2] は外力を表す。
この場合,安定点は, x = n %pi (n は整数)になる。 ただし,n が奇数の場合は振り子が上で止まった場合に対応し, 鞍点のため不安定点となり,
本当に安定するのは n が偶数の場合である。先の例題のように, 「2次の微分方程式は,2つの1次の微分方程式を連立させたもの」 と考え,角速度
w を導入するとともに,さらに,x→x2,w→x1 に置き換えると,
x'' = w' = x1' = - x1 * a / m - sin(x2) * g / (m * L) + F(t) / (m * L)
w = x2' = x1
となる。
外力が加えられた場合
まず関数を用意する。myfunc4 を僅かに手直しするだけである。
関数に引き渡されるパラメタの一つに時刻 t を用意してあるのは,
前出の myfunc4 の時と同様であるが,今回は t を本当に利用している。
それでは早速解いてみる。
次のプログラムは解を求めるものである。
殆んどは前出の myfunc4, p1e4 と同じであり,
変更点は色違い(赤)で示した。
ただし,コメント行については変更があっても特に示してない。
→
<myfunc5.m>
(Download)
|
function xdot=myfunc5(t,x)
xdot=zeros(2,1); % 領域確保
F=0.01*sign(sin(0.998*t));
g=1;
a=0.1;
m=1;
L=1;
xdot(1)=(-x(1)*a + (-sin(x(2))*g + F)/L )/m;
xdot(2)=x(1);
% end of function
|
|---|
% p1e5 - 角度-角速度上の解軌跡と,時間-角度,角速度のグラフ
% 横軸 は 角度 x ... x2,
% 縦軸は角速度 w ... x1.
[x,w]=meshgrid(-.15:0.05:.15, -.15:0.05:.15);
ss=size(x);
dxp=zeros(ss(1),ss(2),2);
dxm=zeros(ss(1),ss(2),2);
for n2=1:ss(2)
for n1=1:ss(1)
dxp(n1,n2,:)=myfunc5(0.001,[w(n1,n2) x(n1,n2)]);
dxm(n1,n2,:)=myfunc5(-0.001,[w(n1,n2) x(n1,n2)]);
end
end
figure(1);
quiver(x, w, dxp(:,:,2), dxp(:,:,1),'r');
hold on;
quiver(x, w, dxm(:,:,2), dxm(:,:,1),'g');
hold off
% 時間領域: 0 --- 200 (秒)
% 初期速度 0, 初期変位 0.01
[tt,xx]=ode23('myfunc5',[0 200], [0 0.01]);
% グラフの重ね合わせ
hold on
plot(xx(:,2), xx(:,1),'b')
hold off
% 解の時間変化をグラフ化。
figure(2); % 2 枚目のグラフ用紙を用意する
plot(tt,xx);
% 振動が安定した後の振幅を求める。
% ただし,表示の半分の時刻で振動が安定したと考えた。
len=length(tt);
len2=round(len/2);
disp('Amplitude = ');
disp(max(xx(len2:len,2))-min(xx(len2:len,2)));
% end |
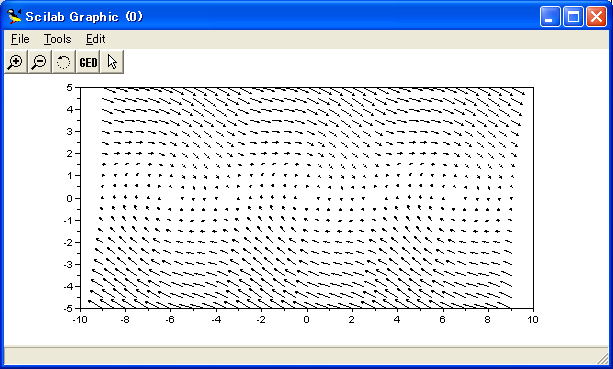
関数内の外力 F は大きさは時間とともに変わる。
従って,変位-速度平面上のベクトルの方向は時間とともに変わるので注意が必要である。
今回の力は sign (符号) 関数で与えられるため,方形波である。
従って,2通りの力の掛かり方しかないため,ベクトルの図は必要十分の2枚書くことにした。
2つのベクトルの方向が同一の場合は,
後から書いた矢印によって,最初に書いた矢印の一部が消されているので,
しまうので注意しよう。
ここで,上記とは異なる非常に長い周期の外力を加えた場合の解を示す。
二通りの外力に応じた二通り場所に収束しているのがわかる。
myfunc5, p1e5 からの変更点は次の1箇所である。
myfunc5 3行目
前出の例 F=0.01*sign(sin(0.998*t));
ここでは F=0.01*sign(sin(0.03* (t-1) ));

こうした外力を受け,上記のプログラムをそのまま走らせた解を示す。
先ほどよりも大きな軌道を描いている。
これは,振り子独自の振動数にちょうど対応する周期の外力を加えたことで,
大きな振幅が得られたのである。
もしも myfunc5 内の 0.967 という数字を,大きくしても小さくしても,
振幅はこの図よりも小さくなる。
(実際に,0.99 とか 0.9 といった値を当てはめて実行させてみよう。)

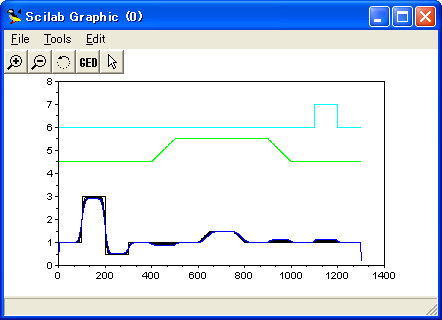
このとき,角度や角速度の時間変化は,次の図の通りである。
なお,初期値が 0.01 のグラフは角度を,0 のグラフは 角速度を表す。
(最初の図は,収束する様子を示す。後ろの図は,発振が始まる様子を示す。)
基本的にグラフは滑らかな曲線であるが,所々に折れ曲がっているような場所が見られる。
これは,外力が変化したところである。


まとめ:外力があったとき,
・定常状態では外力と振子の周期は等しい
・ちょうどよい周期のとき,振子の振幅は最大になる
・振子の性質(質量,振子の長さ,空気抵抗)に応じて,周期が変わる
パラメトリック振動
注意:パラメトリック振動については現在勉強中です。以下の記述は,正しいとは限らない。
パラメトリック振動は,パラメタが時間とともに変化したとき生じる振動である。
振り子の運動に照らし合わせると,時間とともに,例えば振り子の長さ L が変わることに対応する。
振り子とともに長さが変わることは,ブランコを漕ぐ運動の非常に単純なモデル化である。
それでは早速解いてみる。
殆んどは前出の myfunc5, p1e5 と同じであり,
変更点は色違い(赤)で示した。
ただし,コメント行については変更があっても特に示してない。
<myfunc6.m>
(Download)
function xdot=myfunc6(t,x)
xdot=zeros(2,1); % 領域確保
F=0;
g=1;
a=0.1;
m=1;
L=1-.2*sign(sin(2.04*t));
xdot(1)=(-x(1)*a + (-sin(x(2))*g + F)/L )/m;
xdot(2)=x(1);
% end of function
|
% prog1e6 - 角度-角速度上の解軌跡と,時間-角度,角速度のグラフ
% 横軸 は 角度 x ... x2,
% 縦軸は角速度 w ... x1.
[x,w]=meshgrid(-.8:0.2:.8, -.8:0.2:.8);
ss=size(x);
dxp=zeros(ss(1),ss(2),2);
dxm=zeros(ss(1),ss(2),2);
for n2=1:ss(2)
for n1=1:ss(1)
dxp(n1,n2,:)=myfunc6(0.001,[w(n1,n2) x(n1,n2)]);
dxm(n1,n2,:)=myfunc6(-0.001,[w(n1,n2) x(n1,n2)]);
end
end
figure(1);
quiver(x, w, dxp(:,:,2), dxp(:,:,1),'r');
hold on;
quiver(x, w, dxm(:,:,2), dxm(:,:,1),'g');
hold off
% 時間領域: 0 --- 500 (秒)
% 初期速度 0, 初期変位 0.01
[tt,xx]=ode23('myfunc6',[0 500], [0 0.01]);
% グラフの重ね合わせ
hold on
plot(xx(:,2), xx(:,1),'b')
hold off
figure(2);
plot(tt,xx);
% 振動が安定した後の振幅を求める。
% ただし,表示の半分の時刻で振動が安定したと考えた。
len=length(tt);
len2=round(len/2);
disp('Amplitude = ');
disp(max(xx(len2:len,2))-min(xx(len2:len,2)));
% end |
時間とともにゆれが大きくなり,最後には振幅が安定する。
まとめ:ブランコの長さが変わるというパラメトリック振動では,
・定常状態ではブランコの伸び縮みの周期は,ブランコの揺れ周期の半分である
・このブランコの場合,伸び縮みの関数として,
L=1-.2*sign(sin(2.04*t));
L=1-.2*sign(sin(1.96*t));
くらいの範囲がちょうどよい周期である。
ブランコは振れが大きいほど周期が長くなる性質があり,
励起の周期が長い(カッコ内の数字が 1.96 に近い)程,最終的な揺れの振幅は大きいが,
安定点に到達するまでの時間が長い。
一方,励起の周期が短い(カッコ内の数字が 2.04 に近い)程,最終的な振幅は小さいが,
安定点に到達するまでの時間は短い。
ここで示した数字よりも長すぎたり短すぎる励起の周期の場合は,
ブランコはあまりよく振れてくれないようである。
ただし,初期条件によって,これらの性質は変わる可能性がある。
・ブランコの性質(質量,振子の長さ,空気抵抗)に応じて,周期が変わる
以上のように,この節では振動が継続する場合について,
2通りの例題を示した。
ここでは表示をきれいにするためのプログラムを入れたが,
そういうことが不要であれば,極めて少ないプログラミングで,
実用的な問題解決に有効である。
|