MATLAB

back
New '03/12/10 = シンボリックな変数の部分を追加。
Update '03/12/10 = シンボリックな変数の部分を追加。 First '03/12/4 = 新規作成。

MATLAB つかいませんか (File-3) --- MATLAB を使うための ABC --- 応用3 （回路応答を symbolic に求める）
目次 Symbolic Tool 概要数字の取り扱いシンボリックな変数方程式を立てて解く Solve 関数回路理論への応用

Symbolic Tool 概要

Symbolic Math Toolbox を使うと，数式を文字式のまま解いたり，非常に高い精度で数値計算することが可能になります。

注意：以下の実行には，Symbolic Math Toolbox が必要です。

数字の取り扱い

通常	>> 1e20+1-1e20 ans = 0 数学的に考えると答えは 1 の筈ですが， MATLAB の標準的な計算は有効桁数が約16桁なので，数値計算の誤差が現れます。 >> 1e15/3-333333333333333 % 並んだ '3' の数は15個 ans = 0.3125 数学的に考えると答えは 1/3, 即ち小数点以下に 3 が無限に並ぶ筈ですが，数値計算の誤差によりこういう数字が現れます。 >> (1-8/9)*9-1 ans = 4.4409e-016 数学的に考えると答えは 0 の筈ですが，数値計算の誤差により実際の答えは 0 ではありません。
シンボリック演算使用 : sym	>> sym(1e20)+sym(1)-sym(1e20) ans = 1 >> sym(1e15)/sym(3)-333333333333333 % 並んだ '3' の数は15個 ans = 1/3 >> 1-sym(8)/sym(9) ans = 1/9 >> (1-sym(8)/sym(9))*9-1 ans = 0 このように，数値を sym( ) で囲んでやると，数学で普通に考える正しい答えが現れます。 sym でくくられたものはシンボリックなものとして扱われ誤差がないためです。割り切れない割り算は分数のまま残します。例題 >> sym(3)/sym(2.5) ans = 6/5
任意桁数演算使用 : digits, vpa	>> digits(30) 最初にこのように宣言すると，vpa による計算が 30 桁になります。 >> vpa( ' 1e20+1-1e20 ' ,30 ) ans = 1. >> vpa( '1e15/3-333333333333333' ) % 並んだ '3' の数は15個 ans = .333333333333333 % 並んだ '3' の数は15個。15+15→30桁 >> vpa( ' 1-8/9 ' ) ans = .111111111111111111111111111111 % 並んだ '1' の数は30個。 >> vpa( ' (1-8/9)*9-1 ' ) ans = 0 このように，数式を vpa( ' ' ) で囲んでやると， digits( ) で指定した桁数で計算します。計算は10進数のようです。

以上示したように，MATLAB の数値計算は，様々な精度で行えます。ただし，桁数の増加は計算時間も増加します。素早く計算させたいなら，標準の計算をしましょう。

シンボリックな変数

>> syms x y
最初にこのように宣言すると，x と y は文字のまま式で使えます。

>> f=(x-y)*(x+y)*(x^2-y^2)
f = (x+y)*(x-y)*(x^2-y^2)
>> g=f-y^4
g = (x+y)*(x-y)*(x^2+y^2)+y^4
>> h=simplify(g)
h = x^4-2*x^2*y^2
>> pretty(h)

                                  4      2  2
                                 x  - 2 x  y

以上のように，関数 f, g, h は x, y を含んだ文字式です。
なお，simplify は約分等を行う関数となり， pretty は数学の常識的な形式の出力関数です。
なお，simplify のような数式を別の表現に変換する関数には， collect, expand, horner, factor, simple などもあります。

それでは，こうして得られた関数に具体的な数値を代入しよう。
>> u=subs(h,x,2)
u = 16-8*y^2
>> v=subs(h,y,2)
v = x^4-8*x^2
>> subs(u,y,2)
ans = -16
>> subs(h, {x,y}, {1,2} )
ans = -7
>> subs(g,y,x)
ans = -x^4
以上のように，関数 subs により変数の値を代入して式を計算できます。一度に多数の変数へ代入することもできます。また，数値だけでなく，別の変数を代入することもできます。

微積分も可能です。なお，積分では区間を区切った計算も行えます。
>> diff(h,x)
ans = 4*x^3-4*x*y^2
>> int(h,x)
ans = 1/5*x^5-2/3*x^3*y^2
>> int(h,x,0,1)
ans = 1/5-2/3*y^2

方程式を立てて解く

Solve 関数

Solve 関数を使うと，方程式を解くことができます。連立方程式も可能です。ただし，数式内で使う変数は，シンボリックであることを宣言することが必要です。

例
>> syms x
>> kai=solve('0.5=x^2','x')
kai =
[ -.70710678118654752440084436210485]
[ .70710678118654752440084436210485]

回路理論への応用

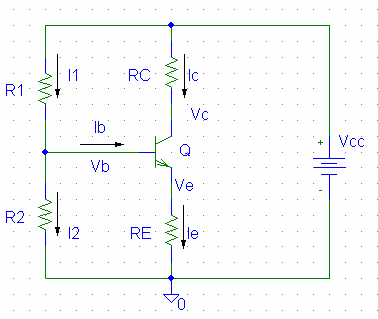
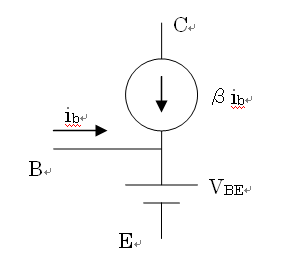
上記の回路について，ib と i2 を，方程式を立てて解いて見ましょう。ただし，トランジスタは右図の通りとします。なお，βについては B という変数で代用しました。（Bは他に「ベース端子」という意味で図にありますが，混同しないように）

>> clear
>> syms i2 ib B r1 r2 re vcc vbe
>> S=solve('vcc=r1*(i2+ib)+r2*i2','vcc=r1*(i2+ib)+vbe+re*(1+B)*ib','ib','i2')
S =
i2: [1x1 sym]
ib: [1x1 sym]
>> S.i2, S.ib
ans =
(r1*vbe+re*B*vcc+re*vcc)/(r1*r2+re*r1+re*r2+re*B*r1+re*B*r2)
ans =
-(r1*vbe+r2*vbe-vcc*r2)/(r1*r2+re*r1+re*r2+re*B*r1+re*B*r2)
>> pretty(S.i2), pretty(S.ib)

                           r1 vbe + re B vcc + re vcc
                   -----------------------------------------
                   r1 r2 + re r1 + re r2 + re B r1 + re B r2
 
                              r1 vbe + r2 vbe - vcc r2
                 -  -----------------------------------------
                    r1 r2 + re r1 + re r2 + re B r1 + re B r2

こうして得られた解（S.i2 と S.ib) について，具体的な値を求めたいなら，各変数に値を代入することです。次に「代入」の操作法を示します。なお，ここでは抵抗は kΩ，電流は mA を単位として計算しましょう。
>> subs(S.i2,{B,r1,r2,re,vcc,vbe},{200,20,3.5,1,12,0.7})
ans = 0.5061
>> subs(S.ib,{B,r1,r2,re,vcc,vbe},{200,20,3.5,1,12,0.7})
ans = 0.0053